On Rose Curves in the Polar Coordinate System

Abstract

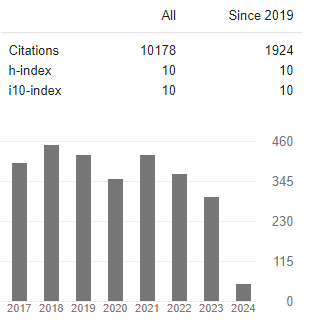
Koji Sakai Milena Sosic

The article examines rose curves in the polar coordinate system, where each rose curve is determined by a cosine function with arbitrary positive amplitude and angular frequency. The amplitude refers to the radius of a circle whose center is the pole in which a rose curve is completely inscribed, and the angular frequency refers to the number of petals of a rose curve. Depending on the values of the angular frequency, which can be an integer, a rational number in the form of an irreducible fraction or an irrational number, the number of petals of a rose curve, the length of the interval for which a rose curve is complete and the polar angle between the peaks of the successive petals of a rose curve are examined. All mathematical considerations are accompanied by suitable examples and pictures.

PDF