Using General Relativity to Explain and Quantify Dark Energy

Introduction

Problem

Dark energy causes the masses in the universe to move apart. Based on the Wilkinson Microwave Anisotropy Probe (WMAP) at NASA, dark energy is estimated to be 71.35% of total energy [1]. Dark energy theories are of different types, as described by Amendola, Misner and Padmanabhan, including quintessence, modified gravity, and cosmic acceleration [2-4]. The LambdaCDM model uses only experimental data in the dark energy theory, providing the value of the cosmological constant Λ in Einstein's field equation. Farnes used a negative mass to explain the dark energy expansion [5]. No current theory explains or numerically predicts dark energy.

Objectives

To explain and quantify dark energy just using the existing theory of general relativity [6-10]. The explanation of dark energy and its associated equations should logically follow from the principles of general relativity. The new explanation should be verified by predicting a percentage of dark energy close to the experimental value.

Summary of Method

When the two masses in Figure 1 travel together under the force of gravity, they gain kinetic energy. Mathematically, two masses are connected by elasticity with a force coming from Newton's law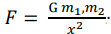. The potential energy, as in any spring, is stored in the elastic of space. If all objects in the universe collapse so they touch, all potential energy is converted into kinetic energy. A polar dark energy equation yields the amount of kinetic energy. The amount, when compared with total universe energy, is approximately 71%. Significantly, this suggests strongly that potential and dark energy are the same. The derivation of the dark energy equation in cartesian and polar coordinates is given in Section 2.

Figure 1: Potential energy between two masses

Newton’s law results in only a small amount of kinetic energy when all objects collapse. However, when all objects collapse to half their distance, the speed of light also halves because the dark energy stays constant while its 1D density doubles. This view is that of an outside observer who is not part of the collapse. The halving of the speed of light makes distances appear halved. Therefore, a distance x appears as x/2. If the ratio of the observed speed of light to the ambient speed of light is c”, then a distance x would now appear as xc”. Substituting this for x in Newton’s ituting this for x in Newton’s law yields a more general Newtonian force law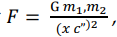thus producing the inverse square law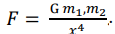, this only applies in a collapsing universe and is responsible for the enormous energy release when all particles are enabled to collapse. THis equation is confirmed by the two-mass theorem in section 9.1.

The universe is built of dark matter, hydrogen, and helium. These atoms are built from electrons and quarks. The electrons are very small and light. However, quarks are heavy and have known upper radius. Therefore, the collapse assumes all quarks collapse into a compact lattice. Just take a quark Q. The dark energy KE is released by the collapse of all other quarks around quark Q. Assuming the mass-energy of a quark is EQ, the dark energy ratio is then given by KE(KE+EQ).

The kinetic energy generated when all mass collapses is described in the method Section 2.

Summary of main results

Section 0 proves the novel inverse fourth power equation   , which calculates the massive inter-mass force when all masses move together in the same proportion.

Section 2 introduces a novel dark energy ratio equation which calculates the enormous kinetic energy released when all masses collapse together into a Gaussian lattice [11].

Section 2.2 introduces an accurate Cartesian dark energy equation which is impossibly slow in calculating the percentage ratio.

Section 2.3 introduces a polar dark energy equation which is concise and efficient.

Section 3 introduces results that predict a dark energy ratio of 71.5% compared with the experimental value of 71.35%.

Methods

General Dark Energy Ratio Equation

For the whole universe, the dark energy ratio is given by:

(2.1)

where   is the total dark energy and E_m

Cartesian Solution to Dark Energy Ratio Equation

Instead of using the mass of the whole universe, it is only necessary to use a single quark Q and the dark energy between this quark Q and all the other quarks. The particles are maximally compressed when they touch in a Gaussian lattice as depicted in Figure 2 and Figure 3 [11]. The total kinetic energy E_sq

originates from the collapse all other quarks onto only one quark

is the total mass-energy of the universe. It is assumed 

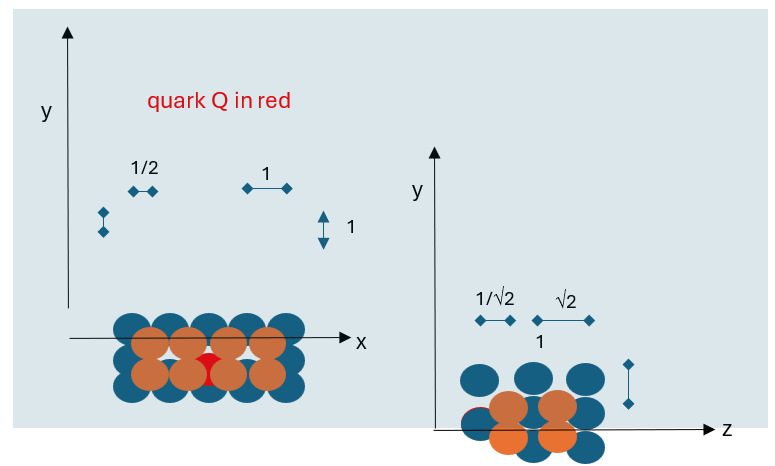
Figure 2: Lattice Plan and Top Elevation

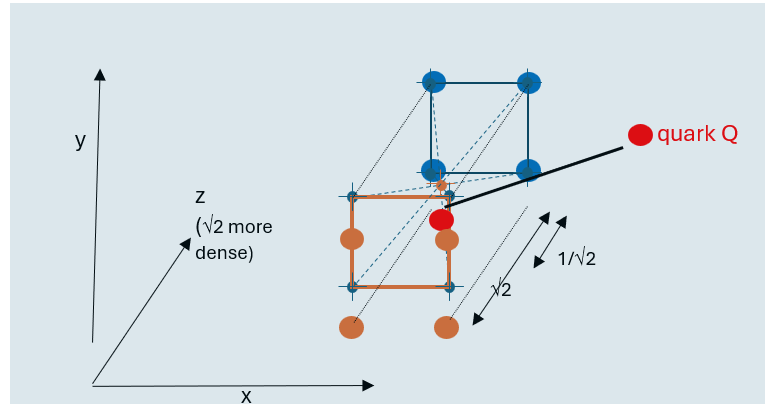
Figure 3: Lattice in Isometric View

Therefore, the dark energy ratio Equation (2.1) can be written as:

(2.7)

The kinetic energy is derived and confirmed in Section 10 and yields Equation (10.1):

(2.8)

                                    with  replacing  and  replacing

This is the kinetic energy generated when all quarks in a radius of  collapse to touch each other, where:

             is derived from Equations (10.2) to (10.5) between quarks in a lattice.

            Layer  is given by Equation (2.35) repeated below:

(2.9)

            The number of quarks  in the universe’s mass is given by:      

(2.10)

            The mass of the quark is given by Equation (8.8).

NOTE: A Cartesian dark energy algorithm is given by restricting  in Equation(2.8) to a maximum of .

Finally, the dark energy ratio is given by Equation (2.7):

(2.11)

where  is the total dark energy given by Equations (2.7) and is the energy in quark Q given by Einstein:

(2.12)

Polar Solution to Dark Energy Ratio Equation
Theorem Polar Dark Energy Equation

The Cartesian Equation (2.8) cannot be computed for all quarks in a reasonable time. However, using polar coordinates, a single compact Equation (2.37) repeated below is used:

,

(2.13)

This equation uses continuous mass distributions rather than discrete in the Cartesian Equation (2.8).

Proof Polar Dark Energy Equation

The total Proof Polar Dark Energy Equationdark energy from a mass pair is given in Equation (9.10):

(2.14)

This is the kinetic energy generated when two quarks move from µ to  is given by:

(2.15)

The radius of the quark Q is  The other quarks are in layers of radius n, as depicted in Figure 4. Layers are defined as multiples of twice the radius of the quark. The distance between two quarks, , is given by:

(2.16)

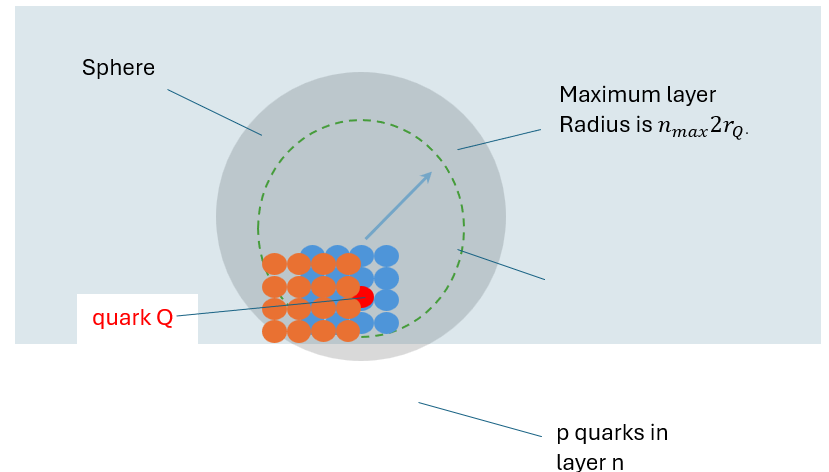
Figure 4:  Sphere with Gaussian Lattice of Particles

When n=1, the quarks are in the first layer where they all touch the central quark Q; therefore, the value of  is twice the radius 2. Substituting  from Equation (2.16) into Equation (2.15) gives the kinetic energy generated for particles in layer n:

		(2.17)
		(2.18)

LET	G' =	(2.19)
\		(2.20)

This kinetic energy is generated when a quark arrives from infinity to layer n, which is distance 2 from quark Q . If   then this is the dark energy released for quarks that touch quark Q. The total energy released by p particles in layer n is obtained by multiplying  by the number of particles p in layer n:

(2.21)

Substituting for  from Equation (2.20) yields:

p

(2.22)

The rate of change of dark energy, needed later, with the number of particles  in a layer given  by:

\

(2.23)

The number of particles in each layer is approximated using the Gaussian lattice as follows [11]. In the gaussian lattice, the spheres are in steps of n = 1 in the x and, y planes. See Figure 2 and Figure 3. In the z direction, they are the height of a square pyramid. The steps of n are then  apart. Consequently, in the z direction, there are Ö2 more quarks than in x and y directions. As depicted in Figure 4, without this compression factor there would only be p particles in a sphere volume of layer radius n:

(2.24)

However, because the z dimension contains Ö2 more particles per n step unit in the z direction, this formula becomes:

(2.25)

The rate of change particles p wrt n is then given by differentiation:

\

(2.26)

The rate of change of dark energy with n is  and is given by:

=

(2.27)

Substituting from (2.23) and (2.26) yields:

(2.28)

\

n

(2.29)

The total energy is then obtained by integrating the above term  yields the total dark energy:

\		(2.30)
\		(2.31)

But ln1 is zero:

\

(2.32)

 

Using  for E yields:

,

(2.33)

The value of pmax is obtained by substituting n=nmax in Equation (2.25) :

\

(2.34)

Rearranging yields:

(2.35)

The number of quarks  in the universe is given by dividing the mass of the universe  by the mass of a quark :

(2.36)

Finally, substitute G' from Equation (2.27), and  from Equation (2.35), in Equation (2.33) yields the dark energy :

(2.37)

                                    where mqis given by Equation (8.8).

QED

Dark energy Percentage (%) Results 

The dark energy ratio is given by Equation (2.7) repeated here:

The term  is given by Equations (2.37). The term  is given by Einstein as . The following data was used:

radius of quark, Zeus [12]              is         4.3E-19 metres,

  mass of up quark [13 ^_]              is         3.82E-30 Kgms.

mass of down quark [13]                     is         8.36E-30 Kgms.

mass of universe [14]        is         1E+53 Kgms.

This equation estimates 71.50% dark energy compared with the total of all energy. This value is close to the experimental value from the NASA WMAP, which estimates dark energy at 71.35% (70.39 to 72.25) [12].

Discussion

Dark Energy Equation

The dark energy equation is solved using polar coordinates to sum the dark energy in layers around a single quark Q. It is only slightly more accurate to scan each quark in the Gaussian lattice using the Cartesian equation [11]. This scan was performed in an informal report for quarks in the nearest 200 layers and gave essentially the same result [15].

Radius of a Quark

The results reveal 71.5% dark energy, assuming the radius of a quark  is given by Zeus which is the actual radius rather than the maximum radius [12]. Using the experimental data of 71.50% backwards in the dark energy equation, the average quark radius is calculated as 4.3E-19 m, which is the experiment value.

Rate of Expansion of Dark Energy

Radiation from stars creates dark energy because the photons lose kinetic energy which is converted into potential or dark energy [16]. The loss of kinetic energy changes the wavelength of the photons. Because all matter can eventually break down into radiation, the final state of the universe is probably just dark energy. The beginning of the universe is likely the reverse. Radiation going backwards in time removes dark energy. As radiation removes dark energy, it must return to a highly compressed form. It is thus consistent with the “Big Bang” theory.

Black Holes
Black holes are concentrations of matter with an event horizon which prevents radiation leaving. The collapsing process used in this paper is very like matter entering a black hole. 

Applying 4th power law to a black hole removes the singularity and time stop problems [17]. Dark energy suggests that photons are micro black holes containing trapped dark energy waves. The same for particles but trapped photons.

Statements and Declarations

The author woThe author declares no conflicts of interest. This work was not supported by any external funding. E. Babb was the sole author of this study. The author has read and approved the final manuscript.

The author would like to thank Sandra S, Peter B ,Richard B, Peter K, Dr. Andrew B , Prof. Volodymyr K, Dr. Hao C, Dr. Tahir, and staff at Imperial college and Oxford university.

Appendices

Average Mass of a Quark

The elementary particle chosen was a quark. Quarks were used as the two masses because they are the heaviest elementary particles. There are many types of quarks, but the main ones are up and down quarks, which inhabit protons and neutrons in equal numbers. It is assumed that there is a single quark Q with an average of mass  of the up and down quarks. The other particle was the electron. This is lighter than a quark but much larger and thus contains much less dark energy. Therefore, it was not used in the calculations in this study.

The universe is composed of 73% hydrogen, 25% helium, and 2% something else [18]. The “something else” may be like hydrogen. The hydrogen atom has one proton, and so two up and one down quark with mass:

(8.1)

The helium atom has two protons and two neutrons and so has mass:

		(8.2)
\		(8.3)

Adding both together in a proportion of 75% to 25% yields:

		(8.4)
		(8.5)
\		(8.6)

Thus, there are 12+9 quarks, yielding a total of 21 in the three hydrogen and one helium atoms. Therefore, the average quark has the mass:

		(8.7)
\		(8.8)

The up quark [13] has a mass of approximately 2.3 MeV (3.82E-30 Kgms ), while the down quark [13] has a mass of approximately 4.8 MeV (8.36E-30 Kgms).

Two-Mass Theorems

The situation which all the masses halve their distance apart is illustrated in Figure 5.

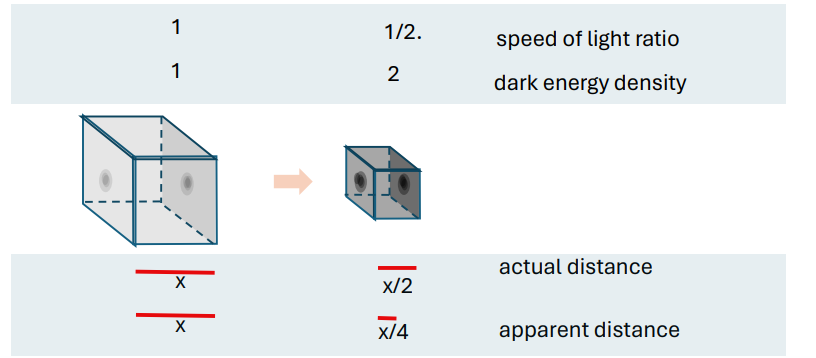
Figure 5: Halving x also Halves the Speed of Light Ratio so Halves x Again

Suppose the side of a unit cube of space between masses is halved. The stored dark energy remains the same, and so its 1D density is doubled. Consequently, the speed of light is halved. An actual distance x is halved as shown. However, halving the distance also doubles the density to 2 and so the speed of light is halved. This means that the apparent or observed distance x which was x/2 is further halved to x/4.

This effect occurs with objects under water. The lower speed of light in water makes objects appear less deep to the outside observer. If the speed of light in water is halved, the apparent depth is halved.

Theorem: Marginal Energy Two Masses

Space is elastic, obeys Newton’s gravity equation, and can store energy released as kinetic energy. The force or marginal change in dark energy for two masses  and  is given by the inverse fourth power from Equation (9.9):

,

(9.1)

The term G has the same size but different dimensions to the standard G.

Proof: Marginal Energy Two Masses

The variable c” is the ratio of the speed of light, c’ to c. The observer is always at c”=1, so everything shrinks relative to him. When the speed of light is c, the force between the two masses  is given by the Newton’s inverse square law:

(9.2)

However, when the speed of light ratio is less than 1, the dark energy density rises and the distance the observer sees is x times the speed of light ratio c". This new value for x called  defined as.

(9.3)

The observed distance between  is now  giving.

(9.4)

Substituting  from equation (9.3) gives:

(9.5)

This is a generalisation of Newton’s law, which includes dark energy density represented by c.” Calculating the total dark energy requires that the entire universe be shrink. Consequently, all masses move together in the same proportion. The drop in the speed of light ratio c,” and so rise in the density of dark energy, causes initial distances  to reduce by ratio c” giving:

(9.6)

For example, if c" = 1/2 then the distance x becomes .

Substituting equation (9.6) in Equation (9.5) yields:

(9.7)

At c”=1 the force  and   must be the same. Therefore, the variable , yielding an extra term  below:

(9.8)

Removing  yields

(9.9)

NOTE: The dimensions (but not the value) of G have now changed. However, it could be called  in the equation above if the reader wants it to have dimensions.

QED1
Theorem: Total Energy Released by Two Masses

The kinetic energy generated and 3D space-energy removed, when m₁ and m₂ move from ¥ to are x_min apart, when all the masses in the universe move simultaneously, is given by Equation (9.10)

(9.10)

Proof: Total energy released by two masses

The total energy is then obtained by integrating the force where F =  for x = x_min to  :

(9.11)

Substituting for  from Equation (9.10) yields:

\		(9.12)
\		(9.13)

However, assuming  <, the second term is negligible and can be removed as follows:

(9.14)

This is the kinetic energy generated when  and  (and all other masses) move from ¥ to  apart.

QED2

Theorem dark Energy for n Masses
Theorem

When spherical particles of equal mass and radius  fall together and surround particle P, they generate kinetic energy  and thus remove of dark energy. They fall together into a lattice where the maximum distance between quarks is 

(10.1)

Proof

The particles are maximally compressed in a Gaussian lattice [11]. This is depicted in Figure 2 and Figure 3. The particles are indexed by for the directions. One unit of is ã??2 rã??_q metres. The target particle Q is at location 0,0,0. In the plane the particles are just one unit apart. In the plane they were 1/√2 units apart. 

The lattice in Figure 2 and Figure 3 describes the position of each particle and, therefore, the associated dark energy. The blue particles in the lattice are just 1 unit or ã??2 rã??_q metres apart. The orange quarks are arranged in the same way but are displaced left and vertically by 0.5 units. In the z direction, it was 1/√2 above the blue layer. The distance d_(i,j,k) of any quark at from the particle Q at <0,0,0> is given by Pythagoras:

Distance in units          (10.2)
     if even   (k)  then  x=i   and    y=j    (10.3)
         (10.4)
              (10.5)
The total energy is found by summing the energy from every quark at to the central quark Q at <0,0,0> using the two-mass Equation (9.14) repeated below:

          (10.6)

Both masses are , so:

\

(10.7)

Therefore, the total dark energy for p_max particle pairs collapsing around particle Q is:

(10.8)

The distance  is derived from distance , defined in Equation (10.2);

Ù

(10.9)

The constraint  0> d _{i,j,k <} n _max  restricts the summation to particles outside particle Q and inside a sphere containing p_max particles and n_max layers in radius. Adding this to Equation (10.8) yields:

	(10.10)
	(10.11)
	(10.12)

Conclusion

The equation predicts the percentage of dark energy at 71.50%. The experimental results from the NASA WMAP study indicate a range of 70.39% to 72.25%, which is sufficiently close to validate the new dark energy equationA new equation is proposed for dark energy stored in the universe. This equation is derived using general relativity plus the assumption that potential and dark energy are the same. The most basic theorem provides an inverse fourth power law for the force between two masses when all masses move together based on a novel generalisation of Newton’s law to include the speed of light. The inverse 4th power equation depends on the Newtons law which is based on experiment.

[12]. Conversely, using experimental data of 71.50% in the dark energy equation yields an average quark radius of 4.3E-19 m, which is the experiment value.

Dark energy makes further predictions or suggestions which will affect future research. When stars generate radiation, the energy in each photon is reduced by the gravitational attraction to the star and so creates dark energy [16]. Dark energy removes the time stop or singularity problem with black holes [17]. Dark energy suggests that photons are micro black holes containing trapped dark energy waves. Dark energy distribution between pairs of masses slightly changes the predicted curvature of space.

Alternative theories explain dark energy by changing general relativity. An example is Farnes who used a negative mass [5]. This new approach makes no such changes.

References

1. Bennett, C. L., Larson, D., Weiland, J. L., Jarosik, N., Hinshaw, G., Odegard, N., ... & Wright, E. L. (2013). Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: final maps and results. The Astrophysical Journal Supplement Series, 208(2), 20.
2. Amendola, L., & Tsujikawa, S. (2010). Dark energy: theory and observations. Cambridge University Press.
3. Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Princeton University Press: Princeton, NJ, USA, 2017; ISBN 978-0-691-17779-3
4. Padmanabhan, T. (2008). Dark energy and gravity. General Relativity and Gravitation, 40, 529-564.
5. Pirzkal, N., Rothberg, B., Ryan, R. E., Malhotra, S., Rhoads, J., Grogin, N., ... & Zakamska, N. L. (2018). A Two-dimensional Spectroscopic Study of Emission-line Galaxies in the Faint Infrared Grism Survey (FIGS). I. Detection Method and Catalog. The Astrophysical Journal, 868(1), 61.
6. Cheng, T.-P. Relativity, Gravitation and Cosmology; Oxford University Press: Oxford, UK, 2010; ISBN 978-0-19-9573646.
7. Einstein, A. Relativity: The Special and General Theory; Martino Publishing: Eastford, CT, USA, 2010; ISBN 1-891396-30-7.
8. Katti, A.N. The Mathematical Theory of Special and General Relativity; CreateSpace Publishing: Scotts Valley, CA, USA, 2017; ISBN 1-5305-0199-7.
9. Einstein, A. The Principle of Relativity; Dover Publications: Mineola, NY, USA, 1952; ISBN 978-0-486-60081-3.
10. Penrose, R. (2006). The road to reality. Random house.
11. Conway, J. H., & Sloane, N. J. A. (2013). Sphere packings, lattices and groups (Vol. 290). Springer Science & Business Media.
12. Bae, K. J., Endo, M., Hamaguchi, K., & Moroi, T. (2016). Diphoton excess and running couplings. Physics Letters B, 757, 493-500.
13. Cho, A. (2010). Mass of the common quark finally nailed down. Science Magazine, 201004.
14. Gaztañaga, E. (2023). The mass of our observable Universe. Monthly Notices of the Royal Astronomical Society: Letters, 521(1), L59-L63.
15. Babb, E. New theory of general relativity giving the percentage of dark energy and solving the black hole time stop problem, https://www.academia.edu/127738030.
16. Babb, E. A Modification to general relativity which calculates the expansion of dark energy, the Hubble constant, at an almost exact 71km/sec/megaparsec, https://www.academia. edu/42186366.
17. Babb, E. A correction to general relativity that removes time and singularity problems with black holes and even gives the radius of a Quark, https://www.academia.edu/99161234 
18. Berkeley Labs. Proportion of hydrogen and helium in the universe.