The Info-Geometric Analysis of Wind Speed Dynamics and How Energy is Influentially Impacted by Information Geometry (IG)

Introduction

IG is a branch of differential geometry focused on using non-Eu clidean geometry for probability theory and stochastic process es. It provides a geometrical background for studying large data sets and probability distributions and defining distances between them. This approach allows for the avoidance of traditional least square methods and instead uses a complete differential geom etry background, within which statistical data sets are analyzed using mathematical concepts. These data sets are compared to mathematical models called "statistical distributions" which are finite dimensional manifolds. A Riemannian geometry framework is then applied to these manifolds to estimate distances between points of interest. The corresponding geodesics, or shortest paths, are used to connect these points. More interestingly, IG statistical manifolds (SMs) parametrization is visualized by figure 1.

The study uses information geometry (IG) analysis to improve the accuracy of weather prediction models, specifically for wind speed forecasts. The Gamma distribution, a statistical model for wind speed, is used to categorize wind speed forecasts within a two-dimensional statistical manifold. Wind speed forecasts are important for various applications, including aviation, naviga tion, and renewable energy. Wind speed probability distribution functions (PDFs) were analysed [3] to determine their usefulness in describing different wind regimes and their potential for wind energy. The study[3] introduced new approximation meth ods for deriving power curves from wind farm data. locations with moderate wind speeds were better served by the Weibull distribution, but locations with low and high wind speeds were better served by the gamma distribution. As seen in figure 2, no location proved a good fit for the Rayleigh function.

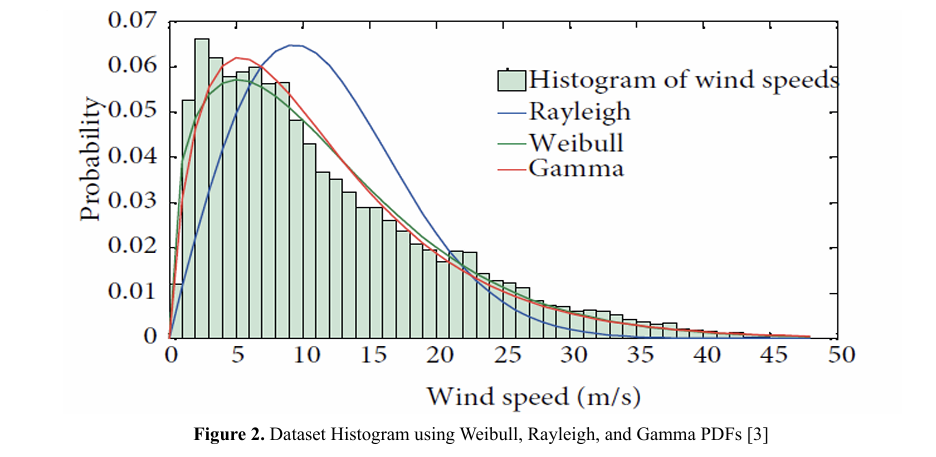
As the wind power business expands into areas with different wind regimes, the results emphasize how important it is to choose a suitable distribution function for determining the wind speed frequency distribution. The paper is organized as follows: Section II contains the necessary IG definitions. Section III discusses the latest findings. An overview of prospective IG applications to energy activities is provided in Section IV. Section V answers potential upcoming research questions, which would pave the way for a pioneering platform of multiple energy research advancements around the world. As a result, this study's innovative contribution to energy researchers is highlighted. Section VI contains concluding remarks as well as potential study routes intertwined with open research topics.

Main Ig Definition

Main Results

Ig Aaplications to Advance Energy

A new method of identifying problems with electric power systems, particularly those with distributed sources was revealed. The method uses a mathematical concept called differential geometry and provides a comprehensive analysis of issues related to such systems. Additionally, the approach uses IG sensitivity analysis of power systems' Differential-Algebraic Equation (DAE) models. A novel IG approach for identifying electric power systems that addresses challenges in optimization models was provided. It includes domain-specific tools to regularize these models and is scalable for large systems due to low effective dimensionality in data space. The method is illustrated using.

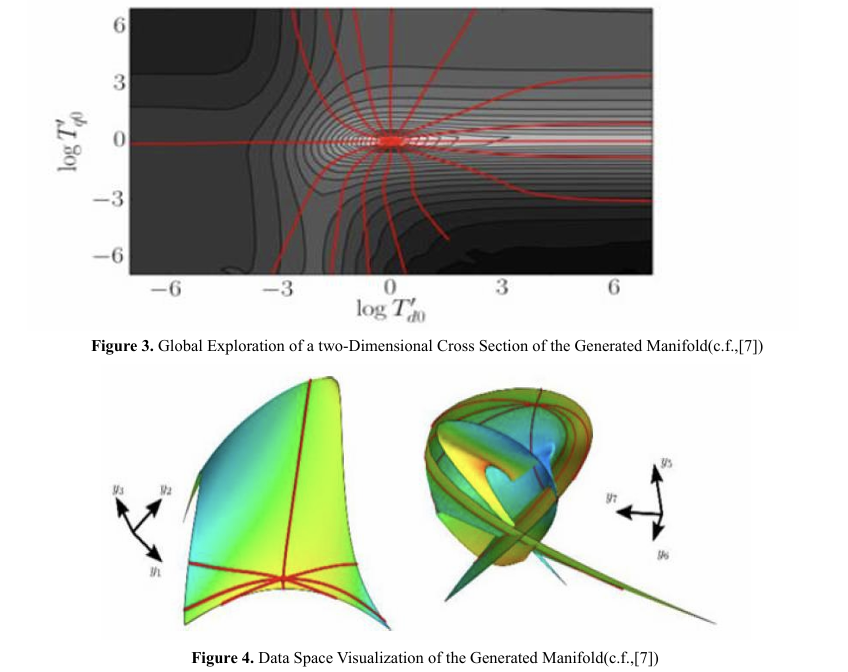
synchronous generator example. Figure 3 (c.f.,) describes a graphical representation of a complex mathematical model by showing different parameters and the likelihood of their joint occurrence. The red lines on the graph are representative of the shortest path between two points on the model manifold. The text also points out that these lines align with specific regions of the cost surface, which are referred to as "canyons". Figure 4 (c.f.,) portrays a visual representation of a model in data space, specifically a two-dimensional cross-section. Red lines show the geodesic curves, which are a subset of curves from figure 3.

More interestingly, a new proposed technique for detecting tar gets in weather clutter using the IG approach was undertaken [8]. Figure 5 describes the results of comparing two methods used for detecting targets in weather clutter. One method uses the Riemann Distance, which calculates a "mean" for a set of data points, while the other uses the Euclidean Distance, a more traditional method.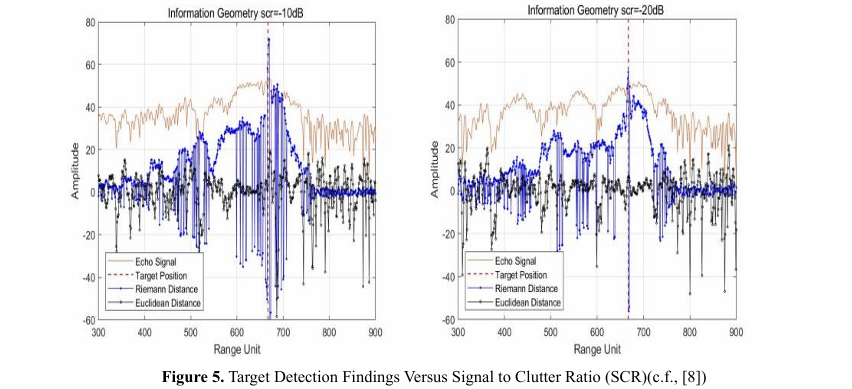

Figure 6 supports strong evidence of how well IG target detec tion works, where many simulations (called Monte Carlo exper iments) were and plotted in a graph [8]. A comparison between the newly proposed IG technique versus constant false alarm rate (CFAR), the traditional way of detecting things, has shown that their new method performed better.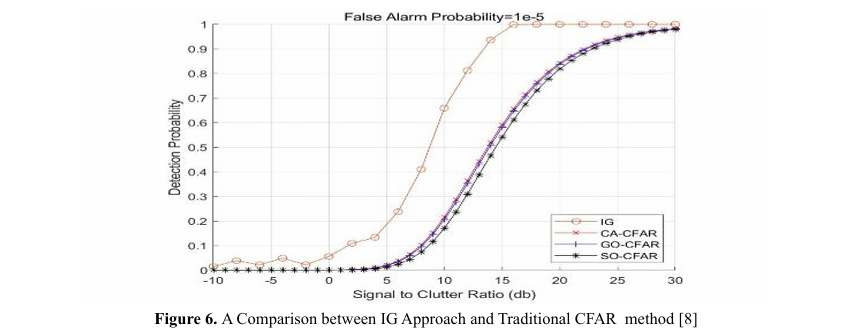

Questions and Open Problems

Question 1

Question 1 Will IG allow information loss in model prediction? Will IG allow information loss in model prediction? In simpler terms, the model manifold (a way of visualizing the model's predictions) keeps all the information about the model's predictions [9,10], while the cost surface in parameter space (a way of visualizing the model's performance) condenses all the information into a single number - the cost.

Question 2
How well can IG separate the model, i.e., the manifold embedding into data space?
In IG, the model can be separated from the data it is fitting. The model can be thought of as a shape embedded in the space of data, while the data is just a point in that space. This abstraction helps study the properties of the model without being tied to a specific observation. However, the cost surface in parameter space is affected by the observation and can be very sensitive to it.

Question 3
How well can IG support labeling for scientific predictions?
The model manifold is a collection of points that stay the same even if the way the model is represented changes [9-12]. The model parameters act like coordinates on this manifold, providing labels for specific predictions without changing the underlying structure of the manifold.

Question 4

Is it possible for IG to act as a natural connection between the local and global analysis? FIM is a way to measure the differences between two models that are just a tiny bit different from each other. This is done using the Riemannian metric on the model manifold[9-12]. It serves to connect the study of local differences between models to the study of global differences.

Question 5

What is the groundbreaking significance of IG language? IG is a way of describing mathematical concepts that work well even when there are a lot of variables to keep track of. This is useful because in some areas of research, the number of vari ables involved can be very high.

Here we overview some potential emerging open problems:

Open problem 1
Having seen the IG is power in modelling. Is it possible to use GEs to replace classical mechanics? In a way, GEs is descriptor of the equations of motion for statistical parameters representing any underlying distribution.

Open problem 2
Is it possible to use IG to analyze the dynamics of time-dependent systems on both macro and micro levels?

Open problem 3
Can the general dynamics of photon states be reinterpreted and geometrically analysed using an IG technique like this one?

Open problem 4
Can new connections be made between the info-geometric analysis of the systems being studied and the Einsteinian Theory of General Relativity (TGR)? This is because IG is tensor-based. Could this be a significant advancement?

Open problem 5
How feasible is it to extend the applicability to Control theory, automotive and Satellite industries. Also, what about the IG role to enhance Electromagnetics, cybersecurity and IoT?

Closing Moments and Next Phase Research

This work is a breakthrough in the field of IG modelling of wind energy since it allows for the geometric analysis of the overall dynamics of several related phenomena, including wind speed forecast and weather prediction models. These collaborations take place within a unified info-geometric platform. Sever al unresolved issues surface from the novel's beginnings as an unprecedented line of inquiry. The next phase of research in volves employing extending the proposed ground-breaking IG approach solving the open problems in section V.

References

1. Mageed, I. A. (2024). Info-Geometric Analysis of Gamma Distribution Manifold with Gamma Distribution Impact to Advance Satellite Earth Observations.

2. Mageed, I. A., & Zhang, K. Q. (2022). Information Geom etry? Exercises de Styles. electronic Journal of Computer Science and Information Technology, 8(1), 9-14.

3. Mageed, I. A., Zhou, Y., Liu, Y., & Zhang, Q. (2023, Au gust). Towards a Revolutionary Info-Geometric Control Theory with Potential Applications of Fokker Planck Kolm ogorov (FPK) Equation to System Control, Modelling and Simulation. In 2023 28th International Conference on Auto mation and Computing (ICAC) (pp. 1-6). IEEE.

4. Mageed, I. A., Yin, X., Liu, Y., & Zhang, Q. (2023, August). $\mathbb {Z} _ {a, b} $ of the Stable Five-Dimensional $ M/G/1$ Queue Manifold Formalism's Info-Geometric Structure with Potential Info-Geometric Applications to Human Computer Collaborations and Digital Twins. In 2023 28th International Conference on Automation and Computing (ICAC) (pp. 1-6). IEEE.

5. Mageed, I. A., & Zhang, K. Q. (2022). Information Geom etry? Exercises de Styles. electronic Journal of Computer Science and Information Technology, 8(1), 9-14.

6. Gomes, E. D. C., Alberge, F., Duhamel, P., & Piantani da, P. (2022). Igeood: An information geometry approach to out-of-distribution detection. arXiv preprint arX iv:2203.07798.

7. Transtrum, M. K., SariÄ?, A. T., & StankoviÄ?, A. M. (2017). Information geometry approach to verification of dynam ic models in power systems. IEEE Transactions on Power Systems, 33(1), 440-450.

8. Sheng, H., & Zhang, X. (2022, August). Weak target detec tion with information geometry in weather clutter. In 2022 2nd International Conference on Frontiers of Electronics, Information and Computation Technologies (ICFEICT) (pp. 77-82). IEEE.

9. Transtrum, M. K., Machta, B. B., & Sethna, J. P. (2010). Why are nonlinear fits to data so challenging?. Physical re view letters, 104(6), 060201.

10. Transtrum, M. K., Machta, B. B., & Sethna, J. P. (2011). Geometry of nonlinear least squares with applications to sloppy models and optimization. Physical Review E, 83(3), 036701.

11. Mageed, I. A., & Kouvatsos, D. D. (2021, February). The Impact of Information Geometry on the Analysis of the Sta ble M/G/1 Queue Manifold. In ICORES (pp. 153-160).

12. Amari, S. I., Barndorff-Nielsen, O. E., Kass, R. E., Laurit zen, S. L., & Rao, C. R. (1987). Differential geometry in sta tistical inference. Lecture Notes-Monograph Series, i-240.