Safety Behavior Analysis of a Delayed Control System

Introduction

A continuous delayed system proposed by A. Uçar is considered for this work to address safety behavior [1]. Time delays that occurred in different science and engineering is becoming a very interest and important topic now-a-days [2-3]. The prototype delayed dynamical system is extensively used as a prototype model to observe oscillation in shipbuilding industry [1, 4-8]. Also, instability and periodic fluctuations phenomena can be explained by this type of time delays system in model systems [9]. Unwanted and unsafe chaotic behavior after a range of system parameter values can be analyzed with this system. This model is extensively used to chaotic study. Also, time delayed arises in different systems in feedback science, engineering and medicine. Delayed differential equations are extensively used in Chemostat system, delayed neutral networks, internet congestion control system and Mackey-Glass equation, musical instruments, communications and control systems etc. Time delayed also occurred due to sensors dynamics in feedback path which correspond to undesirable oscillations and instability [10-15].

Since A. Uçar proposed time delay dynamical system which is very important for feedback science, engineers and control engineering fields, delayed differential equation (DDE) to solve this prototype model is becoming very important and interesting now-a-days. Improvement of his works and systems related to this delayed system are utmost important. A Uçar in his original work has tried to propose his new system for chaos studies as well as show its behavior [1]. In his later work he has tried to show some of chaotic behavior of this delayed dynamical system [16]. Chunguang et. al. has tried to see the behavior for various parameter values of this system [17]. Mingshu has tried to show the behavior of this dynamical system by using Euler method rather than 4th order Runge-Kutta method to reduce error up to certain limit. Karl et al. have tried to synchronize the two types of A. Uçar systems [3, 18, 19].

Authors in this current investigation used self-written 4th order Runge-Kutta code in Matlab to observe the behavior of the system in lieu of using ODE45 solver in Matlab at first for constant values ‘τ’ and ‘d’ but changing values for another constant ‘c’. Behavior is analyzed for very small step size (0.001) to see very smaller change in the system. After that pre-function value was taken smaller than previous value and behavior was observed. Then time delay was changed but all other parameters were remained fixed and the behaviors were observed. Then parameter relations have been tried to find out for similar behavior of the system but for different system parameters. Comparisons were made with others findings.

Objective

The present study aimed to determine the impact of different data ranges which can lead to chaotic behavior on delayed dynamic systems to deal with safety aspects. Since these systems need to be function properly in all the time, however finding these ranges which can cause nonfunctional of these systems are prime importance. It is expected that this finding will increase understanding of complex phenomena involved in delayed dynamical system.

Description of the Model

Delay Differential Equation (DDE) is different than Ordinary Differential Equation (ODE). In ordinary differential equation derivative depends on the current value of the independent variable (assume, t) or for that particular instant value but in delay differential equation, system derivate at a certain time depends on the system at earlier time say t-τ. In this work delay differential equation has been used. DDE have two important terms: ‘preinterval’ and ‘pre-function’. Pre-interval is [-τ, 0] and Pre-function (Initial function) is x_o (t)= Ï?(t) for t ϵ [t_o -τ, t_o].

In this work a prototype delayed system proposed by A. Uçar is considered. It has an autonomous continuous time delayed differential equation with cubic nonlinearity term. Diagrams are provided to show the solutions mode for different model parameters. The rich behavior of this system is numerically illustrated by writing 4th order Runge-Kutta codes.

Numerical Analysis

A. Uçar’s proposed delayed dynamical model is analyzed by using 4^th order Runge-Kutta method. This technique leads better accuracy. Numerical algorithm is provided here as a finite difference scheme. Important steps in using 4^th Order RungeKutta method in this delayed system is mentioned here

Step-1: Function subroutine has been written for pre-function Ï? (t). It will provide data for the function for every change of time in the pre-interval.
Step-2: Values have been provided for c, d and τ
Step-3: Values also have been provided for step size(h)
Step-4: Number of subdivisions provided by using step size that is used in step-3 number
Step-5: Number of subdivisions in the interval [0, τ] has been determined
Step-6: Number of steps(k) in the pre-interval [-τ, 0] is also determined
Step-7: Number of steps(m) in the interval [-τ,tmax] is determined. Here tmax is the maximum value of time up to which solution desired.
Step-8: Pre-function output:

Loop1 i=0 to i=k

t(i+1)= -τ +i*h

x(i+1)=phi(t(i)) end of Loop1
Step-9: Solution output:
Loop2 j=k:m t(j+1)=(j-k)*h
k1=h*(c*x(j-k+1))-d*(x(j-k+1))^3
k2=h*(c*(x(j-k+1)+0.5*k1))-d*(x(j-k+1)+0.5*k1)^3
k3=h*(c*(x(j-k+1)+0.5*k2))-d*(x(j-k+1)+0.5*k2)^3
k4=h*(c*(x(j-k+1)+k3))-d*(x(j-k+1)+k3)^
3 x(j+1)=x(j)+1/6*(k1+k2+k3+k4)
end of Loop2
Step-10: Plot of required data

Results and Discussion

System behavior has been analyzed for system without delay condition and when delay is considered and shown on Figures. As the system gets some delay it oscillates at first then comes to equilibrium position. This is type of system behavior is shown in Figure-2(b). Figures 2 to 4 indicate that as ‘c’ value increases from 0.7 to 1.0 the solution behavior losses its equilibrium and tends to oscillate and orbitally stable limit cycle formed. The periodic behavior of solutions increases as ‘c’ increases. Numerical simulation also indicates that the period of the solution for c=1.2 is longer than that with c=1.0.

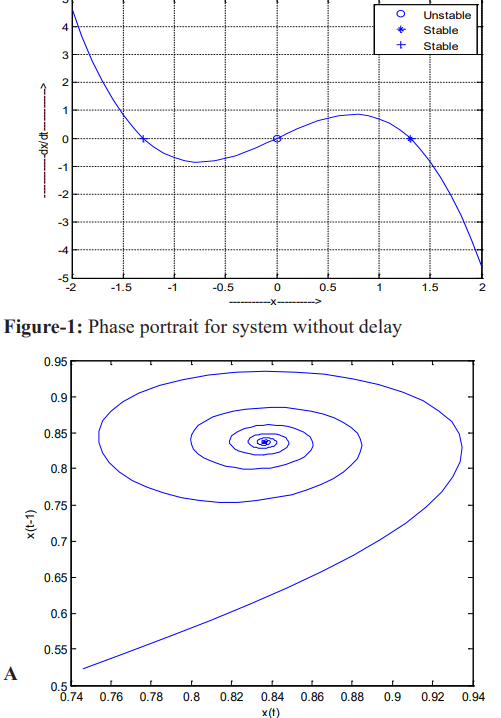
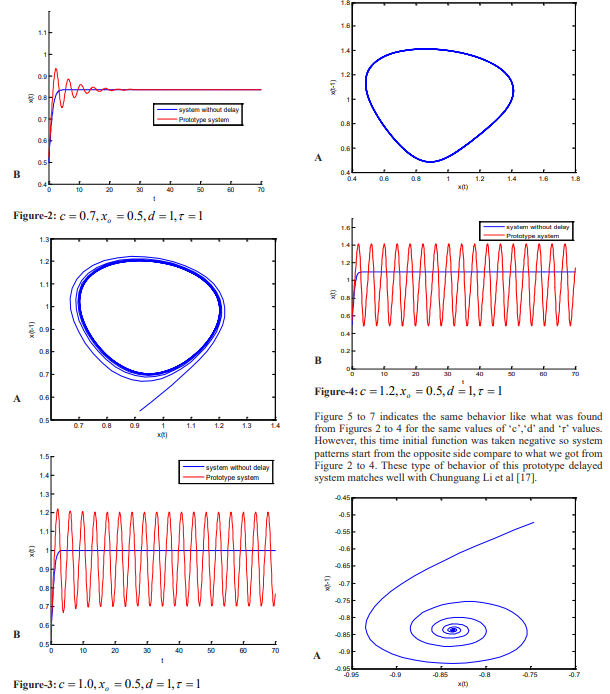
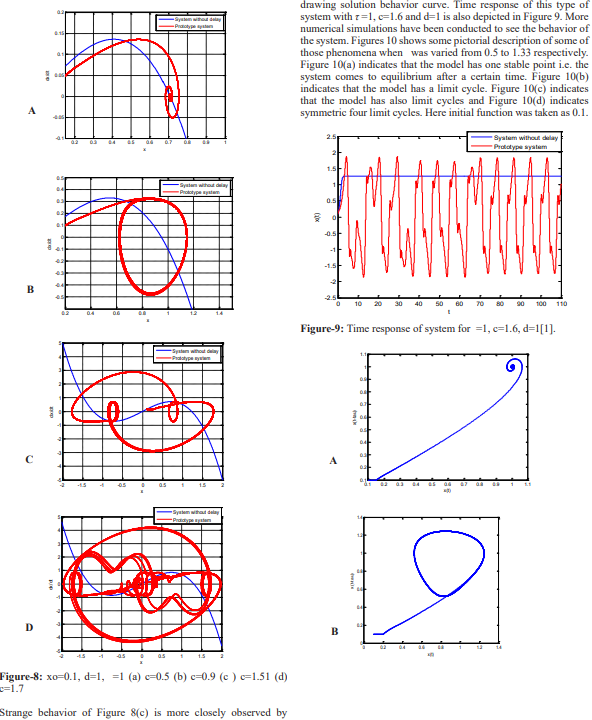
Figure-10: c=1, xo=0.1, d=1(a) =0.5 (b) τ =1 (c) τ =1.3 (d) τ =1.33

Further numerical works have been conducted to see how system behaves with increasing τ is shown pictorially in Figure 11. It seems that when p becomes 1.5 then all oscillations depicted in Figure 10 vanishes and exhibits limit cycle behavior as shown in Figure 11(a). For τ value of 1.6 Figure 11(b) shows chaotic behavior but when τ becomes 1.64 the model comes to simple dynamics depicted in Figure 11(c). But when is chosen 1.72 the model again shows chaotic behavior as shown in Figure 11(d).

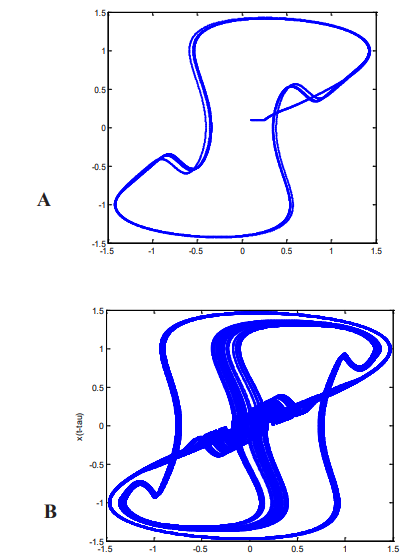
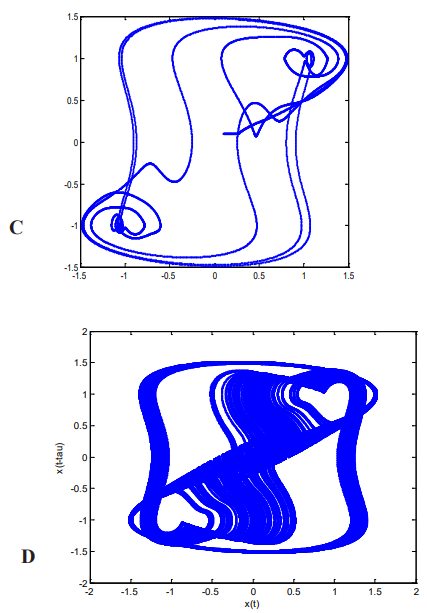
Figure-11: c=1, xo=0.1,d=1 (a) τ =1.5 (b) τ =1.6 ( c) τ =1.64 (d) τ =1.72 As system changes behavior for τ values from 1.64 so trajectory of the system was observed in that particular value. Figure 12 shows a typical trajectory of the model and shows behavior of the system for 0.001 integration step size by writing own 4th order RungeKutta code. The linear and nonlinear feedback gain both fixed at unity with time delay taken as 1.64 values.

Figure-12: typical trajectory of the model for c=1,xo=0.1,d=1, τ =1.64

Up to this point it seems like the system behavior changes with varying parameters might have relation among parameters to have same type of behavior. So, it was needed to find out same type of behavior for different sets of parameters. Also, that could indicate same type of chaotic behavior for a range of parameters. If for a range of parameters chaotic behavior seems same then it is qualitative preserved chaotic behavior (QPCB), otherwise chaotic behavior will be Unique Chaotic behavior (UCB). If there could have a relation like τ=p/c where d is taken as unity then with a fixed value of p values curve be drawn for c vs. τ . Figure -13 implementing this concept. Every line indicates fixed value of p. From Figure-13 it is found that as c value increases τ value decreases

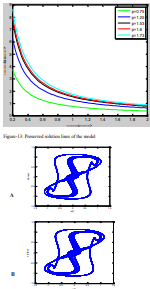
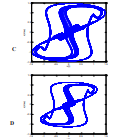
Figure-14: xo=0.1, d=1 (a )c=0.6, τ =2.667 (b)c=0.8, τ =2 (c ) c=1, τ =1.2 (d) c=1.2, τ =1.33

From Figure 11(b) it is found that chaotic behavior occurred for a particular value of c,d, τ values. Now to verify the qualitative preserved of this solution for p=1.6, some more numerical works have been done on that particular case. This time p is taken as constant 1.6 values but c and τ is varied. Figure 14 shows all of this behavior and looks like same chaotic behavior. So, the model exhibit qualitatively preserved chaotic behavior. From Figure 14 it is found that all curves have same structure but different in size. This also indicates that similar beh

Conclusion

In this work behaviors have been analyzed for the A. Uçar prototype delayed dynamical system up to certain extension for various parameter values. Results show that the system behavior more or like predictable up to a certain limit of parameters but shows chaotic behavior after a certain value. Qualitative Preserved Chaotic Behavior was used to observe the system behavior. Qualitative Preserved Chaotic Behavior could be used to analyze chaotic behavior for various systems as well. Results were compared with others findings [19-26] and matches all behaviors analyzed in this work. Step size was taken smaller but smaller value could show better behavior. It is expected that this finding will increase understanding of complex phenomena involved in delayed dynamical system.

Acknowledgement

This study is based upon supports by the UHD (University of Houston-Downtown). The authors greatly acknowledge for the financial support of this work.

References

1. A Uçar (2002) A prototype model for chaos studies, International Journal of Engineering Science, Elsevier 40: 251-258.
2. http://www.cs.uleth.ca/~roussel/nld/delay.pdf
3. L.F. Shampine, S. Thompson (2000) Solving Delay Differential Equations with dde23 http://www.radford.edu/~thompson/ webddes/tutorial.html
4. G Iooss (1979) Bifurcation of maps and applications. NorthHolland, Amsterdam (1979).
5. B Kaymakcalan, V Lakshmikantham, S Sivasundaram (1996) Dynamical systems on measure chain. Kluwer-Academic, Dordrecht (1996).
6. T Koto (1998) Neimark–Sacker bifurcations in the Euler method for a delay differential equation. BIT 39 1 (1998)
7. T Koto (2001) Periodic orbits in the Euler methods for a class of delay differential equations. Comput. Math.
8. S A Kuruklis (1194) The asymptotic stability of xn+1− axn+bxn−k=0. J. Math. Anal. Appl. 188 (1994)
9. S H Strogatz (1994) Nonlinear dynamics and chaos: with application to physics, biology, chemistry and engineering, Addison-Wesley Publishing Company, Massachusetts.
10. S A Levin and R M May (1976) A note on difference–delay equations. Theoret. Popul. Biol.
11. I Melbourne, M Dellinitz, M Golubitsky (1993) The structure of symmetric attractors. Arch. Ration. Mech. Anal.
12. H Richter (2002) The generalized Henon maps: examples for higher-dimensional chaos. Int. J. Bifurc. Chaos 12: 1371- 1384.
13. The MathWork Inc. Matlab Version 5.1. Natic: MathWorks Inc, MA, 1997.
14. S Wiggins (1990) Introduction to applied nonlinear dynamical systems and chaos. , Springer-Verlag, Berlin 1990.
15. Clement E Falbo (1995) Analytical and Numerical Solutions to the delay differential equation, DDE paper, joint meeting of the Northern and Southern California sections of the MAA, San Louis Obispo.
16. A Uçar (2003) On the chaotic behaviour of a prototype delayed dynamical system, Chaos, Solitons & Fractals.
17. Chunguang Li, Xiaofeng Liao, Juebang Yu (2004) Hopf bifurcation in a prototype delayed system, Chaos, Solitons & Fractals 19: 779-787.
18. Mingshu Peng (2004) Bifurcation and chaotic behavior in the Euler method for a Uçar prototype delay model, Chaos, Solitons & Fractals 2004: 483-493.
19. Karl E Lonngren, Er-Wei Bai (2002) On the Uçar prototype model, International Journal of Engineering Science 40: 1855-1857.
20. P Dormayer (1990) The stability of special symmetric solutions of with small amplitudes. Nonlinear Anal. TMA 14 8 (1990)
21. T Faria, LT Magalhães (1995) Normal forms for retarded functional differential equations with parameters and applications to Hopf bifurcation. J. Diff. Eqs 122: 181-200.
22. NJ Ford, V Wulf (1999) The use of boundary locus plots in the identification of bifurcation points in numerical approximation of delay differential equations. J. Comput. Appl. Math 111: 153-162.
23. K P Hadeler (1980) Effective computation of periodic orbits and bifurcation diagrams in delay equations. Numer. Math 34: 457–467.
24. E Hairer, SP Norsett, G Wanner (1987) Solving ordinary differential equations I, Springer series in computational mathematics vol. 8, Springer, Berlin (1987).
25. B L Hao (1989) Elementary symbolic dynamics and chaos in dissipative systems. World Scientific, Singapore 1989: 476.
26. K In’t Hout, C Lubich (1998) Periodic orbits of delay differential equations under discretization. BIT 1998.