Research on optimization of steel plate linear heating line planning based on multi-objective PCA-PSO particle swarm optimization

Introduction

Ships play a very important role in military, transportation, fishery and other fields, and are the main manifestation of a country's economic and military strength [1]. Therefore, developed countries have invested a lot of manpower, material and financial resources to promote the development of the shipbuilding industry. However, shipbuilding is a very complicated process. The manufacture of the hull alone accounts for 50% of the entire process [2]. In the process of hull manufacturing, the 3D curved surface forming of the hull steel plate is one of the most complicated processes [3]. In the steel plate curved surface forming, the linear heating process is the most effective, simplest and most popular process [4]. Therefore, the current mainstream is using linear heating for steel plate 3D forming. However, this process requires workers with 10-20 years of experience to plan the heating line and perform linear heating according to the forming requirements of the target steel plate [5]. Then, according to the forming results of the steel plate, it is compared with the target steel plate, and the second, third or even multiple heating forming heating line planning and heating are performed. This process not only consumes a lot of manpower, but also wastes heating resources, increases the cost of the enterprise, and wastes national energy [6].

At present, due to the high aging population and poor working environment in Japan, there are no young people entering this industry [7]. In this regard, it is urgent to use modern scientific and technological means and artificial intelligence to provide a reliable, accurate and convenient solution to solve the problem of linear heating of hull steel plates. Therefore, this paper proposes a linear heating line planning optimization method for steel plates based on PCA-PSO particle swarm optimization. This method first uses PCA to extract the features of steel plate deformation, reduces the dimension of high-dimensional complex data, and then uses the PSO particle swarm optimization algorithm to optimize the steel plate deformation process. Modeling, finally, the model can plan the steel plate deformation heating line according to the shape of the target steel plate, and give the heating line prediction results.

At present, many scholars have conducted in-depth research and innovation in many aspects of the process of 3D surface forming of steel plates. Wang proposed to study the initial forming of steel plates by hydraulic cold rolling [8]. Cao et al. specifically studied the application of artificial intelligence in metal deformation and provided reliable suggestions for the application of artificial intelligence in steel plate deformation [9]. However, after the initial cold rolling of steel plates, it is far from meeting the requirements of steel plate deformation. It is necessary to further heat the steel plates linearly. In this process, the planning of linear heating lines is the most complex and difficult. Therefore, Wang et al. proposed intelligent prediction of sheet metal forming deformation based on BP neural network and Sparrow search algorithm [10]. Feng Zhiqiang used rough set modeling method to approximate the deformation of ship plates, and combined fuzzy logic and rough set theory to propose a modeling method based on fuzzy rough set [11,12]. Subsequently, Feng et al. established a modeling method for decision-making in sheet metal water-fire forming process based on rough set [13]. However, the accuracy of the model needs to be improved. In order to further improve the accuracy of the prediction of the heating line of steel plate deformation, Zhou et al. established a radial basis function (RBF) proxy model between process parameters and deformation, and used an improved multiobjective particle swarm optimization (MOPSO) method to search for the optimal process parameter set with non-dominated solutions, which has a certain reference value for engineering applications [14]. Now many scholars also use a variety of methods to predict the heating line, such as Dawa and Song et al. use neural networks to predict the forming shape, which has a certain reference value for the heating forming of steel plates [15,16].

Although many scholars have conducted in-depth research and experiments on the forming process of steel plates, the accuracy of prediction and the practical application of engineering need to be improved. The forming process of steel plates is an extremely complex process, and the data generated in the process are complicated, diverse, and large in volume. The final forming is affected by many aspects. The inappropriate model selection not only leads to inaccurate prediction results, but also requires multiple heating, which not only wastes time and manpower, but also wastes energy resources.

Therefore, this study proposes a linear heating line planning optimization method for steel plates based on PCA-PSO particle swarm optimization. After processing the initial data and extracting data features from high-dimensional data, the PSO particle swarm is used to globally optimize the steel plate forming. Through the training and optimization of the model, not only can the heating line be given according to the shape of the target steel plate, but also the repeated heating process can be reduced, which not only improves efficiency but also saves energy, and has certain engineering application value.

Related Work

Study on Heating and Forming of Steel Plate

Linear heating of steel plates has always been the main process for 3D curved surface forming of steel plates. The principle of steel plate forming is to heat the steel plate, which causes uneven heating of the steel plate, and the internal expansion of the steel plate generates stress, which causes the steel plate to deform. The heating deformation of the steel plate is affected by many factors. For example: temperature distribution of the steel plate, heating rate, cooling rate, material properties (density, specific heat capacity, thermal conductivity and expansion coefficient, etc.), thickness of the steel plate, heating method, phase change, internal stress and boundary conditions. Affected by many factors, the deformation of the steel plate due to expansion coefficient, phase change expansion deformation and stress deformation are shown in Formula 1, Formula 2 and Formula 3

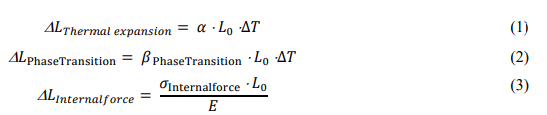
Among them, â??L_{Thermal expansion} is the change of expansion deformation of steel plate, α is the thermal expansion coefficient of steel plate, L₀ is the initial deformation of steel plate, â??L is the change of temperature, â??L_{Thermal expansion} is the change of phase deformation of steel plate, β_{PhaseTransition} is the phase expansion coefficient, â??L_{Internalforce} is the change of stress deformation, σ_{Internalforce} is the internal stress, and E is Young's modulus. However, the change of temperature is affected by heating method, heating radius of heat source and ng method, heating efficiency. Threrefore, the changes of temparature per unit area is shown in formula 4,

Where η represents the heat source efficiency, Q represents the heat source type, L represents the heating length,ν represents the heating rate, and represents q the calorific value. Therefore, the preliminary deformation of the steel plate affected by temperature is shown in formula 5

 Steel Plate Heating Method

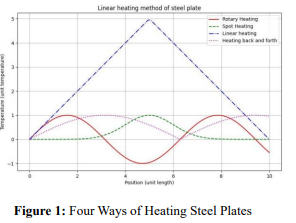
Different heating methods will cause the surface temperature and internal temperature of the steel plate to be different, thus affecting the deformation of the steel plate. For example, Figure 1 shows four heating methods of the steel plate during the phase change process, namely, rotation heating, spot heating, line heating, and back and forth heating. From the figure, we can see that different heating methods lead to different temperatures per unit area of the steel plate.

However, different heating types will also lead to large differences in the temperature between the surface and the inside of the steel plate. Choosing the appropriate heating type can analyze the temperature changes during the heat treatment of the hull steel plate. By analyzing the heating diagram, the process parameters can be optimized, the quality of steel plate forming can be improved, and energy can be used rationally and saved. Figure 2 shows the temperature changes of hull steel plates under different heating conditions with four heating types. They are linear heating, gradient heating, exponential heating and pulse heating. The red line in the figure represents the surface temperature of the steel plate, and the blue line represents the internal temperature of the steel plate.

Figure 2: Temperature Changes of Hull Steel Plates Under Different Heating Conditions for Four Heating Types

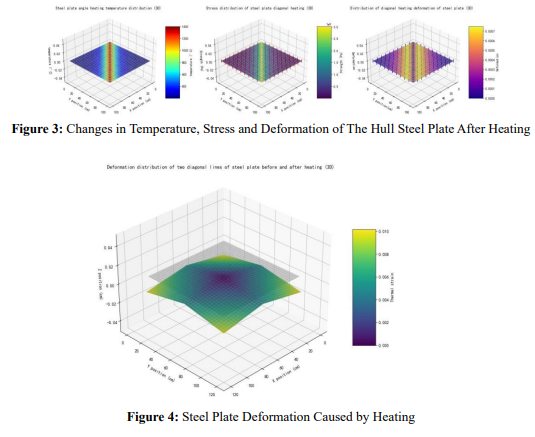
After heating, the steel plate will produce different temperature differences, stress and deformation. As shown in Figure 3, the changes in temperature, stress and deformation after heating a diagonal line of the steel plate are shown. In order to see the deformation of the steel plate more clearly, the deformation of two lines of the steel plate after heating is shown in Figure 4. The figure not only shows the original steel plate, but also the deformation of the steel plate can be clearly seen.

Principal Component Analysis

Principal component analysis (PCA) is a statistical technique proposed by Karl Pearson and later improved by Harold Hotelling and widely used [17,18]. It simplifies the data structure and reduces the data dimension in multivariate statistical analysis while retaining as much original data variation information as possible. PCA can not only convert high-dimensional data into low-dimensional data for visualization and analysis, generate new variables that are independent of each other, remove the correlation between variables and reduce information loss, but also reduce the noise in the data.

In the study of the deformation process of the steel plate, the deformation data of the steel plate is preprocessed first. First, the matrix X is decentralized, as shown in formula 6, and the eigenvalue vector in u. The covariance is calculated as shown in formula 7, and the eigenvalue and eigenvector are obtained, as shown in formula 8, where Λ is a diagonal matrix and V is an eigenvector matrix.There are n samples and p features in the matrix x.

The reduced-dimensional data is obtained by calculating the cumulative contribution of the k principal component, where the calculation of the contribution is shown in Formula 9, and the reduced-dimensional data is shown in Formula 10

PSO Particle Swarm Optimization Algorithm

The Particle Swarm Optimization (PSO) algorithm is an optimization technique based on swarm intelligence. It was proposed by James Kennedy and Russell Eberhart in 1995 and was inspired by the foraging behavior of bird flocks [19]. The PSO algorithm searches for the global optimal solution by simulating the social behavior of individuals (particles) in the search space.

In this study, it is assumed that the objective function of steel plate deformation is the sum of squares of deformation errors, as shown in the formula 11

Among them, x is the vector of design variables, i d is the deformation of the steel plate at i points, and di target is the target deformation.

During the deformation process, the variables arethe heating  temperature at different positions as T, the heating time as t, and the heating time as t, and the heating points at different positions as P. If there are m heating points, the vector of the above variables can be expressed as shown in  formula 12.

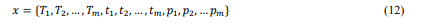
In the process of optimizing the deformation model of the steel plate, a set of particles is first initialized, including the heating temperature, heating time, and heating position. The speed and position of each particle are initialized. The speed and position update formula of the PSO algorithm is used to update the optimal position and the global optimal position of each particle, and the optimal solution is obtained through fitness evaluation and update process. The speed update formula and position update formula are shown in Formula 13 and Formula 14.

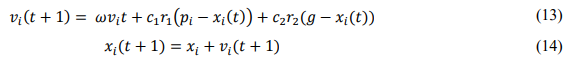
Among them, v_i (t + 1) is the speed of particle i at time t, x (t) i is the position of particle i at time t, and ω is the inertia weight, which controls the influence of the particle's previous speed on the current speed. c₁ and c₂ are learning factors that control the degree to which the particle follows the personal best position and the global best position. r1 and r₂ are random numbers uniformly distributed between (0,1) to increase the randomness and exploration ability of particles, pi is the best position found by particle i so far, and g is the best position found by all particles so far. The pseudo code of this process is shown in Table 2

 Table 2: PSO Particle Swarm Pseudo Code

Experiment

Data Generation

At present, due to some confidential issues in the shipbuilding process, there is no public data set for experiments and research. Therefore, the experimental data of this study uses ANSYS simulation software to simulate the actual operation process of workers and generate relevant data. The simulation data process and ideas are shown in Figure 5. After the worker gets the target deformation design drawing, he plans and draws the heating line of the steel plate based on experience, and then heats it according to the heating line. After multiple heating comparisons, the final target shape is obtained. ANSYS can simulate the entire process. First, the heating line is planned according to the desired target shape, and then the heating line is heated. The steel plate is deformed to the target deformation, and the corresponding data of the entire process is exported, including the heating position, node temperature, node deformation, etc. In the simulation data process, in order to ensure the effective transfer of temperature, a certain heat flux is added per unit area. The simulation data in this study is that the steel plate size is 1000mm* 1000mm* 20mm, and the steel plate is meshed, the mesh size is 20mm* 20mm* 20mm, and the data of 18003 nodes are obtained. The simulated deformation process of a steel plate is shown in Figure 6.

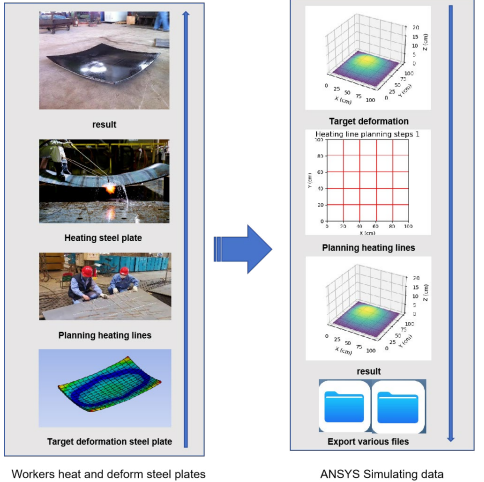
Figure 5: Data Simulation Process

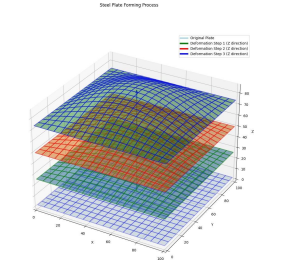
Figure 6: Data Simulation of Steel Plate Deformation Process

Establishment of Multi-Objective PCA-PSO Algorithm Model

The multi-objective PCA-PSO particle swarm optimization algorithm model is to pre-process the data generated by the simulation, first reduce the dimension of the high-dimensional data, extract features, and reduce the data dimension as much as possible without losing information, so as to reduce the amount of calculation for the subsequent particle swarm modeling and improve the training efficiency. According to the characteristics of the particle swarm and the ability of global optimization, a global optimization model is established and trained. After the trained model, the target deformation data is input into the model, and the model can plan the heating line and give the results. The model establishment structure is shown in Figure 7.

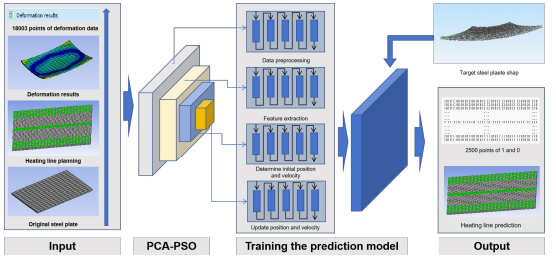
Figure 7: Multi-Objective PCA-PSO Algorithm Structure Diagram

In order to verify the quality of the model, it is necessary to use the mean square error to evaluate the accuracy of the model. The mean square error is actually a loss function of the error between the predicted features and the expected value. Its loss function is shown in Formula 15.

Among them, θ is the parameter obtained by multi-objective PCA-PSO optimization, yÃÂ??i (θ) is the predicted value based on the parameter, and yi is the true value.

In the process of 3D curved surface forming of steel plates, the planning of heating line planning has a great influence on the quality, efficiency and cost of forming. The multi-objective PCAPSO algorithm can optimize from multiple objectives to obtain the optimal solution. However, the genetic algorithm simulated annealing algorithm also has the ability of a global optimization algorithm and can find the optimal solution or a solution close to the optimal solution. Therefore, the study compared multiple algorithms. The results are shown in Figure 8.

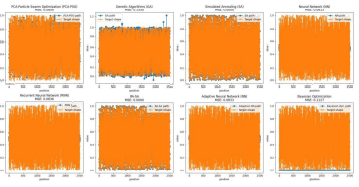
Figure 8: Comparison of Various Algorithms for Predicting Steel Plate Deformation Heating Line

The multi-objective PCA-PSO particle swarm optimization algorithm model after training has a good effect. Compared with the loss function values of various algorithms, the multi-objective PCA-PSO algorithm has the smallest value, indicating that the predicted value of the model is closest to the true value. In other words, the linear heating line predicted by the model is the best.

Discussion

This study uses the multi-objective PCA-PSO particle swarm optimization algorithm to model and plan the heating line according to the target shape steel plate. And by comparing multiple algorithms such as genetic algorithm, simulated annealing algorithm, neural network algorithm, recurrent neural network, adaptive neural network and Bayesian optimization, according to the results, the multi-objective PCA-PSO particle swarm optimization algorithm has the smallest loss function, so it can be preliminarily concluded that the model of this algorithm has good performance. The heating line can be planned relatively accurately. It has great use value in engineering applications. As shown in Figure 9, the input steel plate target shape is shown, and the model can give the heating line. (The input of this process is the steel plate target deformation data, not the deformation picture of the steel plate).

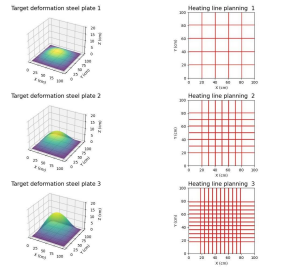
Figure 9: Prediction of steel plate deformation heating lin

Conclusion

The main research content of this paper is the optimization of linear heating line planning for steel plates based on multi-objective PCA-PSO particle swarm optimization. In the traditional linear heating process of steel plates, it mainly relies on experienced workers to heat, the working environment is harsh, the working time is long, and the processed steel plates are uneven. Multiple processing leads to a waste of time and energy. Therefore, the method proposed in this paper plans heating according to the target shape through the multi-objective dimensionality reduction particle swarm optimization algorithm. The heating line results given by this method can assist workers in heating and deforming steel plates to a large extent. It not only reduces the workload of workers and improves work efficiency, but also reduces energy waste and makes reasonable use of resources. It provides reliable application value for engineering applications.

In the future, linear heating of steel plates will face greater challenges and opportunities. How to realize the full automation of the linear heating process of steel plates, including linear planning, linear heating, forming comparison, etc. In the future, the author will continue to conduct in-depth research to provide reliable research for the full automation of the heating and deformation process of steel plates.

Acknowledgement

This work was supported by JST, the establishment of university fellowships towards the creation of science technology innovation, Grant Number JPMJFS2122.

References

1. Walker, T. R., Adebambo, O., Feijoo, M. C. D. A., Elhaimer, E., Hossain, T., Edwards, S. J., ... & Zomorodi, S. (2019). Environmental effects of marine transportation. In World seas: an environmental evaluation (pp. 505-530). Academic Press.
2. Okubo, Y., & Mitsuyuki, T. (2022). Ship production planning using shipbuilding system modeling and discrete time process simulation. Journal of Marine Science and Engineering, 10(2), 176.
3. Xu, L. Z., Shen, W., & Yan, R. J. (2019). Predictive and control models of the spring-back in thick hull plate forming. International Journal of Material Forming, 12, 603-614.
4. Das, B., & Biswas, P. (2018). A review of plate forming by line heating. Journal of Ship Production and Design, 34(02), 155-167.
5. Wang, S., Dai, J., Xu, Z., Wang, J., Li, R., & Wang, J. (2023). Deflection Intelligent Prediction for High-Strength Steel Saddle Plate Forming Applicable to Reducing Ship Weight. Materials, 16(17), 6028.
6. Schwarzmayr, P., Birkelbach, F., Walter, H., Javernik, F., Schwaiger, M., & Hofmann, R. (2024). Packed bed thermal energy storage for waste heat recovery in the iron and steel industry: A cold model study on powder hold-up and pressure drop. Journal of Energy Storage, 75, 109735.
7. Zhang, D., Chai, F., Luo, X., & Shi, Z. (2024). Effect of Reheating Temperature on the Microstructure and Properties of Cu-Containing 440 MPa Grade Non-Tempered Ship Plate Steel. Materials, 17(7), 1630.
8. Wang Shun. "Research on the Prediction of Process Parameters of Water and Fire Bending Based on the Deflection and Deformation of Ship Shell Plate"[D]. Dalian University of Technology, 2018. DOI: CNKI: CDMD: 1.1018.138228.
9. Cao, J., Bambach, M., Merklein, M., Mozaffar, M., & Xue, T. (2024). Artificial intelligence in metal forming. CIRP Annals.
10. Wang, S., Wang, J., Xu, Z., Wang, J., Li, R., & Dai, J. (2024). Deformation Intelligent Prediction of Titanium Alloy Plate Forming Based on BP Neural Network and Sparrow Search Algorithm. Journal of Marine Science and Engineering, 12(2), 255.
11. Zhi-Qiang, Feng, et al. "Modeling Based on Fuzzy Rough Set with Application to Prediction of Line-heating Deformation." Ship Engineering (2016).
12. Torkul, O., Turgay, S., Å?iÅ?ci, M., & Babacan, G. (2023, May). Prediction of Heart Disease Using Fuzzy Rough Set Based Instance Selection and Machine Learning Algorithms. In International Symposium on Intelligent Manufacturing and Service Systems (pp. 699-709). Singapore: Springer Nature Singapore.
13. Feng, Z. Q., Jiao, Z. Q., Chen, S. B., Han, J. F., Han, X. X., Yang, R. D., & Liu, C. G. (2019). On rough Set-Based modeling and with application to process decision for forming plate by line heating. Journal of Ship Production and Design, 35(03), 289-296.
14. Zhou, H. G., Wang, Z., Li, L., & Xu, B. (2022). Line heating process parameter forecasting method based on optimization concept. Advances in Mechanical Engineering, 14(3), 16878132221086689.
15. Yona, D. M., Kori, T. H., Santhosh, A. J., Ashok, N., Thilak, G., Afresa, A. J. A., ... & Tamene, Y. (2023). Prediction of metal deformation due to line heating; an alternative method of mechanical bending, based on artificial neural network approach. Materials Today: Proceedings.
16. Song, J., Lee, J., Kim, D., Kim, W. D., Kang, T. W., Kim, J. Y., ... & Ko, K. (2022). Cycle-Time Estimation for Forming Curved Plates Using Neural Networks. Journal of Ship Production and Design, 38(03), 129-139.
17. Pearson, K. (1901). LIII. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin philosophical magazine and journal of science, 2(11), 559-572.
18. Hotelling, H. (1931). The generalization of Student's ratio.
19. Zomaya, A. Y. (Ed.). (2006). Handbook of nature-inspired and innovative computing: integrating classical models with emerging technologies. Springer Science & Business Media.