Reinforcement Learning DDPG Algorithm Based Wheeled Mobility Aid Robot Control Methods

Introduction

In recent years, with increasing aging, the elderly show significant physiological decline, limb flexibility and other basic abilities, increasing the risk of falls. Meanwhile, as people's lifestyles change, there are more and more lower limb motor dysfunctions caused by sports injuries, traffic accidents, or diseases, making there a huge demand for intelligent assistive devices [1]. Walking robots for the elderly and patients with lower limb motor dysfunction can be categorized into two types: exoskeleton robots and wheeled assisted walking robots [2]. However, the center of gravity control of most exoskeleton rehabilitation robots is not satisfactory, and the safety of the rehabilitation process cannot meet the requirements [3]. Wheeled walking robot itself has a stable chassis, not only can well avoid the patient in the training process due to the center of gravity is not stable and caused by the fall and other secondary injuries, but also in a narrow space to achieve any direction of movement, to give the patient a good sense of spatial movement and real walking experience, wheeled walking robot with its stable chassis and flexible spatial movement ability, in terms of safety and practicality with the Advantages [4].

When using wheeled walking robots for rehabilitation training, due to the complexity of the external environment, the wheeled walking robots are required to follow the desired trajectory as much as possible, which requires the robots to be able to track an ideal trajectory with a time function according to the actual position and motion state, and complete the tracking of each point in the trajectory according to the time requirements Therefore, this paper applies the reinforcement learning algorithm to the traditional proportional-integral-derivative (PID) controller to realize adaptive PID parameter tuning in order to adjust the robot position more accurately so that the robot can complete trajectory tracking.

Although the traditional PID control has the advantages of simplicity of use, easy to implement, no static error, etc., its disadvantage is that it cannot realize the online adjustment of parameters, so when it encounters a strong interference, it is bound to have the phenomenon of prolonged recovery time and increased overshooting, which affects the stability of the motion of the chassis of wheeled robots. A large number of scholars have conducted research on adaptive PID, and introduced the idea of online parameter adjustment in the traditional PID, which improves the response speed of the system. At present, adaptive  PID control methods mainly include: fuzzy PID controller, the method requires a large amount of a priori knowledge, there are parameter optimization problems; neural network-based adaptive PID control, the method can be achieved without identifying the complex nonlinear system to achieve effective control, but in the use of supervised learning to optimize the parameters, the acquisition of the teacher's signals is relatively difficult; evolutionary algorithm adaptive PID controller, the method, although the acquisition of a priori knowledge of the lower requirements, but the computation time is longer, it is difficult to achieve real-time control in practical applications; reinforcement learning adaptive PID controller, proposed the Actor-Critic algorithm to achieve adaptive tuning of PID parameters, which makes use of AC algorithms of model-free online learning [5-8]. The algorithm utilizes the model-free online learning capability of AC algorithm, but the convergence speed of AC algorithm is slow and the training time is long.

In this paper, we adopt the deep deterministic policy gradient (DDPG) algorithm, which is based on the Actor-Critic (AC) framework, to enhance the performance of the PID controller and the deep Q-network (DQN) algorithm is added on the basis of the deterministic policy gradient (DPG) algorithm. This algorithm can not only update in a single step like DQN, but also has the advantages of high data utilization and fast convergence of DPG. In order to realize the adaptive adjustment of PID parameters, a PID controller based on DDPG algorithm is proposed. In the simulation experiments, the kinematic model of the omnidirectional chassis of the wheeled walking robot in our laboratory is used to verify the superiority and generality of the proposed method.

Proposed Method

This section will introduce the kinematic model of the wheeled walking robot chassis. Then, it will describe the design principles and structure of the adaptive PID controller that combines the DDPG algorithm and the PID controller.

Kinematic Modeling of Assistive Robots The schematic and kinematic model of the robot's omnidirectional wheel chassis is shown in Fig. 1. Taking the world coordinate system xw ow yw as a reference, the robot moves in the motion coordinate system xoy with a velocity of magnitude v toward an angle α from the Yw axis. Vx ,Vy denote the horizontal and vertical travel speeds of the robot relative to the motion coordinate system, respectively [9].

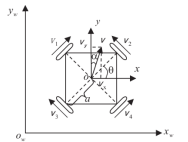
Figure 1: Kinematic modeling of assistive robots

When the robot is moving in any direction, e.g., at an angle α from the y-direction with velocity v, the magnitudes of the horizontal and vertical velocities of the robot respectively:

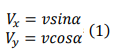
Let the angle between the omnidirectional wheels and the x-axis, measured from the center of the robot chassis, be θ ,and the distance from the center of the chassis to the four wheels be a, then the wheel speed of each omnidirectional wheel is degree is:

Incremental PID Control Principle

Digital PID control can be categorized into two types: positional PID and incremental PID. incremental PID does not require the use of the accumulated value of past deviations, which effectively reduces the system's computational error. Incremental PID is an algorithm that realizes PID control by controlling the increment. The formula is as follows:

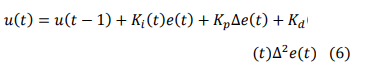
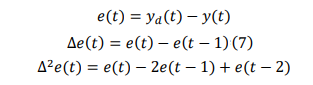
In these equations, yd (t) denotes the current actual signal value, y(t) denotes the current system output value of the current system, e(t) denotes the output error of the system, â??e(t) denotes the first difference of the error, and â??² e(t) denotes the second difference of the error.

The use of incremental PID controllers in control system design can optimize the use of computational resources. The method relies only on the last three sampling points to determine the control increments, thus reducing the computational burden and storage requirements. This facilitates fast training of the DDPG algorithm and storage of sample data. In addition, the incremental PID controller ensures stable operation in the event of a system failure, and since its output is the changing value of the control quantity, it makes the rewards obtained in a reinforcement learning environment more stable, which in turn accelerates the convergence of the algorithm.

In summary, the incremental PID algorithm is used to realize the trajectory tracking control of the wheeled robot, which requires the design of two PID controllers, i.e., the transverse position X controller and the longitudinal position Y controller, and the block diagram of the control system is shown in Fig. 2. The input of the transverse PID controller is xe , i.e., the transverse deviation of the wheeled robot system; the output is vx , the transverse speed of the wheeled robot system. the output of the PID controller goes to the speed distribution controller, which calculates the speeds of the four omnidirectional wheels according to Eq. (2) to correct the transverse deviation of the wheeled robot. The principle of longitudinal position Y control is the same as the principle of transverse position X control, i.e., ye is the longitudinal error, vy is the longitudinal velocity.

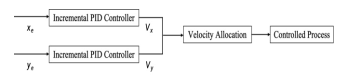
Figure 2: Block diagram of two PID controller system

DDPG Algorithm

Reinforcement learning is a machine learning method that learns behavioral strategies through trial and error, while deep learning is a machine learning method that performs high-level abstraction and feature extraction through multi-layer neural networks. Deep Reinforcement Learning combines the feature extraction capability of Deep Learning with the decision-making capability of Reinforcement Learning to autonomously learn and improve the performance of decision-making strategies. DDPG (Deep Deterministic Policy Gradient) algorithm is an optimization algorithm based on the Actor-Critic algorithm5 framework, which is able to better select the optimal policy in continuous actions such as robot movement. The DDPG algorithm is based on deterministic policy gradient and refers to the experience pool replay mechanism and Double-Depth Q-Network (DDQN) objective network method to update the network parameters and realize the self-tuning of PID parameters, and its algorithm structure is shown in Fig. 3.

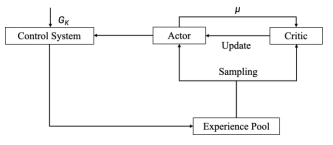
Actor gives a new parameter μ according to the strategy network, denoted as at = μ(S_t â??θ_μ ) + N_t , where θμ denotes the parameter of the neural network, Gk denotes the noise.After one update iteration, the state changes from S_t to S_t+1, and obtains the reward Rt . (S_t , A_t , S_t+1, Rt ) is stored in the experience pool.Finally, samples are drawn from the experience pool to train the strategy network and evaluation network.

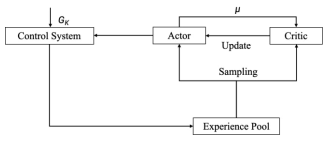
Figure 3: Block diagram of DDPG algorithm structure

The strategy network and evaluation network are updated as shown in Fig. 4. The actor and the Critic consist of two identical networks, denoted as: actor evaluation network μ(s|θ^μ), actor estimation network μ' = (st â??θ μ' ), Critic evaluation network Q(s, a| θQ), Critic estimation network Q' (s, a | θ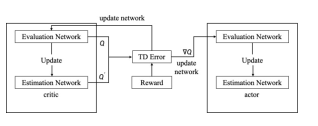Q' ) Q'.

Figure 4: Updating network parameters

The actor evaluation network updates the parameters according to the following objective function

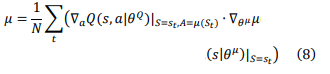
General Structure of Adaptive PID Controller Based on DDPG Algorithm

The design idea is to combine the DDPG algorithm on the basis of incremental PID controller, so the structure design is shown in Fig. 5

Figure 5: Adaptive PID controller based on DDPG algorithm

The system block diagram is based on the traditional PID with the addition of closed-loop control by the DDPG algorithm. The speed allocation module allocates the speeds of the four wheels according to Eq. (2), and the scores are obtained through a selfdesigned reward function , and output to the DDPG algorithm. According to the state obtained by the system output, the DDPG algorithm continuously carries out trial and error training until it selects the action group with the highest score, which is the optimal PID parameter, and outputs it to the two PID controllers, adaptively adjusts the parameter, and the error under the parameter is minimized, and the parameter outputs it to the speed allocation module, and then outputs the speeds of the four wheels to the wheeled walking robots' chassis system, which realizes the trajectory tracking control. The controller uses the parameter vector of the PID controllers, i.e. the 6 parameters to be tuned by the two PID controllers, as the action space.

Critics rate each reinforcement learning cycle using the system's state variables and the defined reward function Rt to generate the TD error δ_TD (t) and evaluate the value function Qt , where δ_TD (t) is provided directly to the actor and Critic, and the reward Rt is used to evaluate the quality of the current behavior.

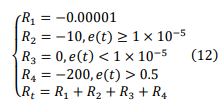
R₁ is the reward for the speed of the four wheels, which is set to a score that has less impact on the system since the main reward comes from the error rather than the amount of control. R₂ and R₃ denote the scores when the error is lower or higher than the error tolerance interval, respectively, and R₄ denotes the score of -200 when the system error is more than 0.5. Finally, the four scores are summed up to form the final reward function. Based on the continuous trial-and-error training, the maximum reward value is obtained, and thus the optimal PID parameter values are obtained.

Simulation Experiment

In this paper, trajectory tracking control simulation experiments are carried out in python environment. Based on the chassis modeling of the wheeled walking robot, the system simulation model was established in Simulink. In the simulation process, the initial position of the controlled object is set as [0,1], the desired trajectory is set as a cosine curve along the x-axis, and the sampling time is set as 1ms. The parameters of the adaptive PID control based on the DDPG algorithm are listed in Tables 1 and Table 2.

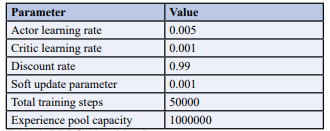
Table 1: DDPG Algorithm Parameters

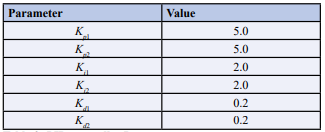
Table 2: PID controller Parameters

Results

Experiment shows the simulation results of trajectory tracking realized by traditional PID controller in the Fig.6. The solid line shows the desired trajectory and the dashed line shows the tracked trajectory. It can be seen that the method can also realize the trajectory tracking, the overshoot is 4.5%, and the tracking trajectory is far away from the target trajectory, and the error is large. Fig.7 shows the simulation results of trajectory tracking control using the PID controller based on DDPG algorithm proposed in this paper. The overshoot of this method is 2.7%, and the trajectory is closer to the target trajectory with less error than the traditional PID control.

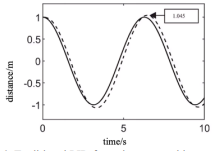
Figure 6: Traditional PID for trajectory tracking

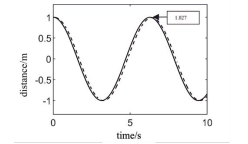
Figure 7: PID control for trajectory tracking based on DDPG algorithm

Compared with the traditional PID controller, the maximum error of this controller is reduced by 48.12%, as listed in Table 3. In addition, the controller's overshoot is reduced by 40% compared to a traditional PID controller, which improves user safety during assisted walking and training.

Table 3: Comparison of results

Comparative results show that the controller is able to track the desired trajectory more accurately when the user uses the wheeled mobility aid robot for rehabilitation training. It also has a strong anti-interference ability due to the trial-and-error mechanism of reinforcement learning, which increases the safety and comfort of training.

Conclusion

In order to ensure that the elderly and patients with lower limb dysfunction can move accurately according to the pre-set desired trajectory when they use wheeled walking robots for rehabilitation training in complex environments, this paper proposes a reinforcement learning method that combines the DDPG algorithm with a PID controller. This method not only solves the problem that the traditional PID cannot adjust the parameters online, but also reduces the storage space requirement of the controlled system, thus reducing the computation time of the system. Simulation results show that the PID control based on the DDPG algorithm has the advantages of high tracking accuracy, small overshooting amount and strong adaptability, which enables the wheeled walking robot to realize accurate trajectory tracking control. The method has good generality and generalization.

References

1. Hou, Z. G., Zhao, X. G., Cheng, L., Wang, Q. N., & Wang, W. Q. (2016). Recent advances in rehabilitation robots and intelligent assistance systems. Acta Automatica Sinica, 42(12), 1765-1779.
2. Zhou, J., Yang, S., & Xue, Q. (2021). Lower limb rehabilitation exoskeleton robot: A review. Advances in Mechanical Engineering, 13(4), 16878140211011862.
3. Neuhaus, P., & Kazerooni, H. (2000, April). Design and control of human assisted walking robot. In Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065) (Vol. 1, pp. 563-569). IEEE.
4. Nokata, M. (2004). Safety Evaluation Method of Rehabilitation Robots. Advances in Rehabilitation Robotics (Springer), 178- 185. 5. Savran, A. (2013). A multivariable predictive fuzzy PID control system. Applied Soft Computing, 13(5), 2658-2667.
6. Chen, J., & Huang, T. C. (2004). Applying neural networks to on-line updated PID controllers for nonlinear process control. Journal of process control, 14(2), 211-230.
7. Saad, M. S., Jamaluddin, H., & Darus, I. Z. M. (2012). Implementation of PID controller tuning using differential evolution and genetic algorithms. International Journal of Innovative Computing, Information and Control, 8(11), 7761- 7779.
8. Pomerleau, A., Desbiens, A., & Hodouin, D. (1996). Development and evaluation of an auto-tuning and adaptive PID controller. Automatica, 32(1), 71-82.
9. Mollaret, C., Mekonnen, A. A., Lerasle, F., Ferrané, I., Pinquier, J., Boudet, B., & Rumeau, P. (2016). A multi-modal perception based assistive robotic system for the elderly. Computer Vision and Image Understanding, 149, 78-97.