Portfolio Optimization through a Multi-modal Deep Reinforcement Learning Framework

Introduction

Algorithmic trading has evolved significantly with the advent of artificial intelligence (AI) and machine learning (ML), enabling data-driven strategies that adapt dynamically to mar- ket conditions. Deep Reinforcement Learning (DRL), particularly, has shown promise in developing autonomous trading agents capable of making real-time decisions by learning from historical market data and simulated environments. Among various DRL methods, Proximal Policy Optimization (PPO) stands out for its balance of learning stability and exploration, making it well-suited for financial markets characterized by volatility and complexity.

This study proposes a Multi-modal DRL framework that integrates algorithmic trading signals derived from technical indicators with Long Short-Term Memory (LSTM)-based price forecasts. This dual approach aims to enhance the agent’s decision-making process by combining rule-based trading in-sights with predictive analytics. The framework is evaluated against baseline models and other reinforcement learning techniques, demonstrating its potential for real-world trading applications. The remainder of this paper is organized as follows: Section 2) Discusses related work in algorithmic trading and DRL applications. Section 3 introduces the proposed framework, detailing the integration of trading signals and price forecasts. Section 4 presents the experimental setup and results. Finally, Sections 5 and 6 provide a discussion of limitations and future research directions.

Related work

Literature Review

Deep Reinforcement Learning (DRL) has become a powerful method for tackling sequential decision-making challenges, particularly in the dynamic and complex environment of financial markets. The versatility of DRL algorithms has been explored extensively in equity trading, portfolio optimization, and trade execution, demonstrating significant potential to enhance trading strategies. This section provides a focused review of Proximal Policy Optimization (PPO) and other leading DRL algorithms, assessing their respective strengths and limitations in financial contexts. PPO is ultimately selected for this study due to its robust performance and stability in managing volatile market conditions. The integration of DRL into algorithmic trading has gained considerable traction, with research showcasing the effective ness of models such as Deep Q-Networks (DQN), Double DQN, and Actor-Critic methods in executing profitable trading strategies [1,2]. While these models have achieved encouraging results, many focus narrowly on a single modality, such as price movements or technical indicators. This limited scope may hinder an agent’s adaptability to diverse market scenarios, especially during regime shifts or unexpected market changes.

Recent advancements have introduced Multi-modal approaches that incorporate additional features like sentiment analysis and macroeconomic indicators alongside price data [3]. These methods enhance prediction accuracy by offering a broader market perspective. However, they often encounter challenges related to data quality and the complexity of integrating heterogeneous data sources, underscoring the need for more sophisticated frameworks. Our proposed approach builds on this research by combining algorithmic trading signals with Long Short-Term Memory (LSTM)-based price forecasting, establishing a comprehensive framework that captures historical market patterns while leveraging predictive insights for informed decision-making. While LSTM architectures have been effectively used for price prediction in previous studies, the novelty of our research lies in integrating these predictive signals with rulebased trading strategies within a PPO-driven DRL framework [4]. This holistic approach aims to enhance trading performance through more stable and risk-aware investment strategies.

Proximal Policy Optimization (PPO) is an on-policy actorcritic method that improves training stability via a clipping mechanism in the policy objective function. This technique effectively balances exploration and exploitation by preventing large policy updates, an essential feature for financial trading where market conditions can shift rapidly. Empirical studies have demonstrated PPO’s effectiveness in portfolio manage- ment, achieving superior riskadjusted returns compared to traditional models, and showcasing robust performance in high-frequency trading (HFT) scenarios [2,5].

Conversely, developed DQN, combining Q-learning with deep neural networks [6]. Although DQN has proven effective in discrete action spaces, it is less suitable for continuous decision-making, which is often required in financial trading. For instance, when applied to stock trading, DQN showed sub-optimal performance due to its limited action granularity [7]. Furthermore, its offpolicy nature can lead to instability, particularly in scenarios with sparse or noisy reward signals, as seen in sentiment-based trading strategies.

Improvements over DQN include Twin Delayed Deep De terministic Policy Gradient (TD3), proposed by, which addresses overestimation bias through delayed critic updates and target smoothing [8]. TD3 has shown promise in continuous action spaces, including trade execution and portfolio rebalancing [9]. However, its reliance on meticulous tuning and a tendency to overfit to short-term signals could reduce profitability in long-term investment strategies.

Soft Actor-Critic (SAC), developed by, optimizes policy entropy to promote exploration [10]. SAC has been effectively applied to trading environments, managing high-dimensional action spaces and adapting to uncertain market conditions [11]. While SAC’s entropy maximization encourages diverse trading strategies, it may lead to excessive exploration, potentially causing inefficiencies when stability and consistency are critical for maximizing equity returns.

Link to Financial Economics

Based on the literature review, PPO offers significant ad- vantages in financial applications, including:

• Training Stability: Maintains performance in volatile market conditions.
• Balanced Exploration and Exploitation: Avoids large, destabilizing policy updates.
• Versatility: Supports both discrete and continuous action spaces.
• Reduced Risk of Local Optima: Essential for maximizing long-term returns.

The proposed framework aligns with the Adaptive Market Hypothesis (AMH), which posits that market efficiency evolves over time as participants adapt to changing conditions [12-14]. By using Deep Reinforcement Learning, which inherently learns from historical feedback to adjust strategies dynamically, our model operationalises AMH in a practical trading system. The integration of multiple data modalities further enhances the system’s ability to detect and respond to regime shifts, consistent with AMH principles.

Considering these benefits, PPO is chosen as the core algorithm for this study. Our experiment will assess PPO’s effectiveness within a Multi-modal DRL framework for portfolio optimization, benchmarking its performance against traditional trading strategies to validate its robustness and potential for delivering superior equity returns.

Our research advances existing methodologies by inte- grating algorithmic trading signals with LSTM-based price forecasts within a PPO-driven framework. This innovative approach not only enhances predictive accuracy but also fosters more stable and risk-aware decision-making, contributing to the evolving field of algorithmic trading.

Methodology

This study analyzed historical data from 29 Dow Jones Industrial Average (DJI) stocks, excluding Visa Inc. due to missing data.

Daily closing prices from September 2, 2003, to August 30, 2023, were collected using Python’s yfinance library. The first 50 data points were excluded to enhance the accuracy of technical indicators.

The dataset was split 90:10 into training (November 11, 2003, to September 1, 2021) and testing (September 2, 2021, to August 30, 2023) subsets to evaluate model performance on both historical and recent market data.

Custom DRL Framework

A custom Deep Reinforcement Learning (DRL) framework was developed using the FinRL library, simulating real-world trading environments. The agent, utilizing the Proximal Policy Optimization (PPO) algorithm, aimed to maximize rewards through optimized trading strategies in a simulated OpenAI Gym environment.

The framework’s state space included market features like cash balance, owned shares, closing prices, trading volume, log returns, and technical indicators (e.g., EMAs, Bollinger Bands, MACD, RSI). The action space allowed buying, holding, and selling actions with constraints reflecting institutional trading practices.

The reward function, based on portfolio log returns, encouraged strategies that balanced profitability and risk management. Realistic transaction costs (0.1% per share) and a buy/sell limit of 30 shares per stock were included to mimic actual market conditions.

Overall, the DRL framework enabled efficient learning and adaptation to dynamic market scenarios, promoting robust and effective trading strategies.

Multi-modal DRL Framework

This study introduces a Multi-modal Deep Reinforcement Learning (DRL) framework that combines Algorithmic Trading Signals and Long Short-Term Memory (LSTM) Price Forecasts to enhance trading performance.

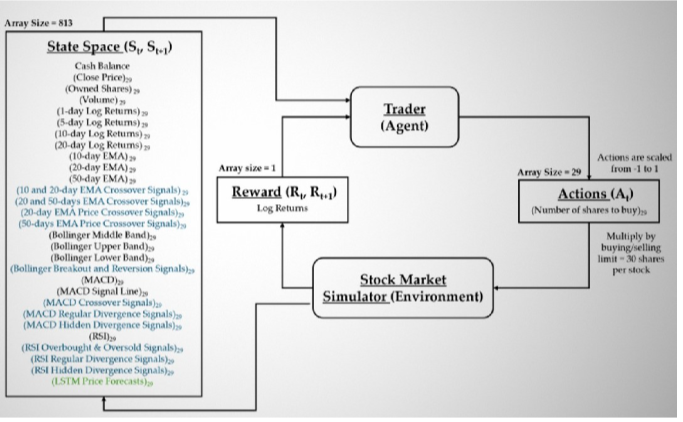
Figure 1: Multi-modal DRL Framework

1) Algorithmic Trading Signals: As illustrated in Figure 1, the proposed architecture seamlessly integrates traditional technical indicators with custom algorithmic trading signals. This integration equips the DRL agent with rule-based insights into market trends, enhancing its ability to make informed trading decisions. The following trading signal strategies are implemented to guide the DRL agent’s decision-making process, delivering structured insights while effectively mitigating the impact of noisy or lagging indicators:

• Moving Average (MA) Crossover: Signals are generated when short-period MAs cross above or below longperiod MAs, utilizing Exponential Moving Averages (EMAs) for improved responsiveness.
• Price Crossover: Indicates momentum shifts by assessing the positioning of the closing price relative to MA values, offering insights into potential trend reversals.
• MACD Crossover: Detects momentum changes through the interaction between the Moving Average Convergence Divergence (MACD) line and the signal line, helping to identify bullish or bearish shifts.
• RSI Overbought & Oversold: Anticipates market reversals by evaluating the Relative Strength Index (RSI) against predefined thresholds, signaling when assets may be overbought or oversold.

These signals are encoded as binary values, enhancing the agent’s ability to interpret market conditions with reduced susceptibility to market noise.

2) LSTM Price Forecasts: The LSTM models generate 1-day forward price forecasts using a 20-day historical sequence. Each stock in the dataset has a dedicated LSTM model trained consistent training and testing sets to maintain evaluation integrity.

The architecture includes two LSTM layers (80 units each) and uses the Adam optimizer with a 0.01 learning rate for effective convergence. As shown in Figure 2, the predicted AAPL price trend closely aligns with historical market data.

The train scores for most stocks range from 0.79% to 2.19%, indicating relatively low error during training. The test scores show greater variability, with some stocks exhibiting much higher.

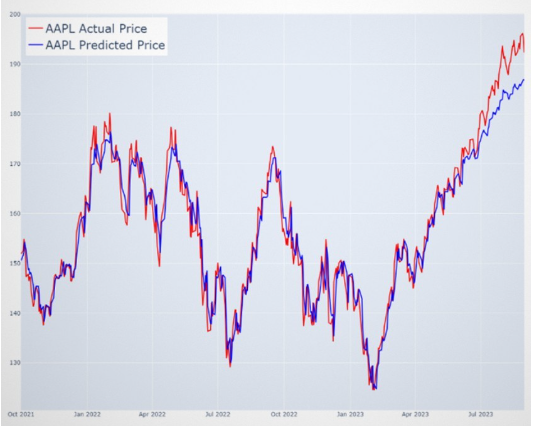
Figure 2: AAPL Price Prediction

While others remain stable, like JNJ (0.81%) and KO (1.58%). Stocks such as IBM (0.96%), JNJ (0.79%), and PFE (1.07%) performed well with low error in both phases, while others, such as XOM (7.53%) and MCD (2.75%), demonstrated a significant gap between training and testing, indicating challenges with generalization. This suggests that the LSTM model performs consistently for certain stocks, but shows difficulty in generalizing for others. Stocks with larger discrepancies between training and testing errors may require further model refinement.

The average MAPE scores highlight the overall model performance during both phases. The higher average test error (1.91%) compared to the train error (1.25%) may suggest potential overfitting or issues with generalizing the model to new data.

Deep Reinforcement Learning (DRL) Algorithm

The proposed Deep Reinforcement Learning (DRL) frame-work leverages the Proximal Policy Optimization (PPO) algorithm, renowned for its stability and efficiency in dynamic trading environments. The PPO agent was meticulously trained to formulate optimal trading strategies by maximizing cumulative rewards within a simulated OpenAI Gym environment.

The PPO algorithm employs a clipped objective function to ensure controlled policy updates, thereby enhancing the stability and reliability of the training process. The neural network architecture incorporates two hidden layers, each with 64 units, and utilizes the Adam optimizer with a learning rate of 0.003 alongside a discount factor of 0.99.

These carefully considered architectural choices enable the model to seamlessly adapt to both stable and volatile market conditions, delivering consistent and robust performance across diverse trading scenarios. The sophisticated integration of algorithmic trading signals and LSTM-based predictive in-sights within the PPO framework further amplifies its efficacy in executing advanced trading strategies.

In conclusion, the deployment of the PPO algorithm within this Multi-modal DRL framework exemplifies a methodologically sound approach to quantitative trading. It demonstrates a balanced blend of profitability and risk management, contributing to enhanced data-driven decision-making and superior portfolio optimization.

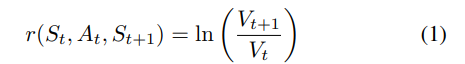
1) Reward Function Rationale: The reward function is a critical component of the Deep Reinforcement Learning (DRL) framework, designed to guide the trading agent towards optimal strategies by quantitatively evaluating its actions. In this study, the reward function is formulated as the logarithmic return of the portfolio value when transitioning from state S_t to state S_t+1 following action At :

where V_t and V_t+1 represent the portfolio values at the current and subsequent timesteps, respectively.

The choice of the logarithmic return as the reward metric is underpinned by several key considerations:

1) Stabilizing Learning: The logarithmic function compresses the range of potential rewards, effectively mitigating the impact of extreme portfolio fluctuations. This stabilization contributes to a smoother learning curve and prevents the agent from being disproportionately influenced by isolated, high-return trades.
2) Risk Sensitivity: By naturally penalizing negative returns and enhancing sensitivity to drawdowns, the log return aligns with risk-adjusted performance metrics commonly used in quantitative finance, such as the Sortino and Sharpe ratios. This feature encourages the agent to adopt strategies that balance profitability with risk management.
3) Compounding Effects: The additive property of log returns simplifies the computation of multi-period returns, supporting the agent’s capacity to model the compounding nature of investment growth accurately. This approach is particularly advantageous for evaluating strategies over extended trading horizons.
4) Handling Negative Portfolio Values: Unlike linear returns, logarithmic returns are not defined for non-positive portfolio values, inherently preventing the agent from strategies that could lead to complete portfolio depletion. This built-in safeguard promotes more conservative and sustainable trading behaviors.
 5) Robustness Against Market Volatility: The log transformation reduces the skewness of returns distribution, enhancing the agent’s robustness in volatile market conditions. This property enables the DRL model to main-tain stable performance across diverse trading scenarios.

Overall, the adoption of a log-based reward function not only aligns with best practices in financial modeling but also ensures that the DRL agent’s decision-making process is both rational and aligned with real-world trading objectives. This approach fosters a more strategic, risk-aware trading behavior, contributing to the achievement of superior risk- adjusted returns in our experimental evaluations.
 

2) Hyperparameter Selection Rationale: The hyperparameters for A2C, DDPG, and PPO were primarily adopted from the FinRL framework, which provides empirically validated defaults for financial applications [15]. PPO’s learning rate (0.0003) and step size (2048) were selected to balance sample efficiency and training stability. The discount factor γ = 0.99 ensures future rewards are sufficiently weighted. All models used the Adam optimizer for its robustness to noisy gradients. These settings were tuned minimally to avoid overfitting and maintain generalisability

Experiments

The experimental framework was meticulously designed to evaluate the performance and robustness of the proposed Multi-modal Deep Reinforcement Learning (DRL) model, uti- lizing Proximal Policy Optimization (PPO). The experiments were conducted in a controlled trading simulation environment, leveraging historical market data from 29 Dow Jones Industrial Average (DJI) stocks over a 20-year span (2003-2023). This extensive timeframe captured diverse market conditions, including bullish trends, bearish downturns, economic crises, and high volatility periods.

Experimental Setup

The trading environment was developed using the FinRL library within the OpenAI Gym framework. This setup provided realistic market simulations, feeding the agent with market observations and assessing the impact of trading decisions. The model utilized daily closing prices, technical indicators (e.g., EMAs, Bollinger Bands, MACD, RSI), and predictive signals from Long ShortTerm Memory (LSTM) models to enhance trend forecasting.

The dataset was divided into training (90%) and testing (10%) sets, with the training phase spanning 2003 to 2021 and testing from 2021 to 2023. The testing period included market disruptions like the COVID-19 pandemic, offering a robust scenario for assessing model resilience.

Technical Signal Encoding Rationale

Technical indicators such as moving average crossovers, RSI, MACD, and Bollinger Bands were selected for their widespread use in quantitative trading literature. Signals were encoded as binary features (e.g., bullish/bearish crossover = 1/-1, otherwise 0), which were then combined with price features and normalized to ensure compatibility with the DRL agent’s input space. This encoding scheme preserves signal interpretability while facilitating integration into neural architectures.

Model Training

The PPO model was trained over 50,000 timesteps using the Adam optimizer (learning rate 0.003). The architecture included two hidden layers (64 units each) and employed Generalized Advantage Estimation (GAE) for improved stability. To ensure consistency, the experiments used 10 different random seeds, reducing the impact of stochastic elements on model performance.

Evaluation Metrics

Model performance was assessed using key quantitative finance metrics

• Annualized Return: Calculates the compounded growth rate of an investment over the evaluation period, providing a standardized measure of performance.
• Sharpe Ratio: Measures risk-adjusted returns by comparing the excess returns of a strategy to its annualized volatility, helping to evaluate the reward per unit of risk.
• Sortino Ratio: Similar to the Sharpe Ratio, but focuses on downside risk by comparing excess returns to the annualized downside standard deviation, offering a more nuanced view of risk-adjusted performance.
• Maximum Drawdown (MDD): Represents the maximum observed loss from a portfolio’s peak to its trough during the evaluation period, highlighting the potential for significant losses.
• Volatility (Annualized Standard Deviation): Analyzes the variability of returns by calculating the annualized standard deviation of returns, providing insights into the stability and risk associated with the investment strategy.

Transaction Cost

In real-world markets, executing trades incurs transaction costs. To mirror actual market conditions, a transaction cost of 0.1% per share is applied. For example, buying 5 shares of a particular stock at a price of $100 a share will incur a transaction cost of $0.50

Results

Performance of the Multi-modal DRL Solution

All experimental evaluations were conducted on a personal laptop equipped with a 13th Gen Intel® Core™ i9-13900H Processor, NVIDIA GeForce RTX 3050 4GB Laptop GPU, and 16GB RAM. Each experimental run required approx-imately 30 to 60 minutes, ensuring robust testing across multiple scenarios.

PPO outperformed A2C and DDPG significantly in terms of both returns and risks, which is reflected in the risk-adjusted metrics, i.e. Sharpe Ratio and Sortino Ratio. This is despite PPO taking more trades and incurring more transaction costs, which is an indication that the model has been able to learn the intrinsic dynamics of the market and making the right trades by buying stocks with higher predicted growth at the right time and selling them appropriately.

As shown in Figure 3, the Multi-modal DRL solution demonstrates superior portfolio performance. The proposed approach, which integrates the Deep Reinforcement Learning (DRL) Proximal Policy Optimization (PPO) model with Algorithmic Trading Signals and LSTM Price Forecasts, delivered outstanding performance. The model achieved an annualized return of 16.24%, a Sharpe Ratio of 0.86, and a Sortino Ratio of 1.27, outperforming other tested modalities. While the standard deviation of 17.49% was marginally higher, the superior returns effectively justified this risk level.

A deeper analysis indicated a notable performance enhancement when Trading Signals were incorporated into the PPO model. However, when only Price Forecasts were utilized performance declined. This discrepancy may be attributed to the limited availability of compatible information and patterns within the state space when solely relying on Price Forecasts, constraining the model’s learning capacity.

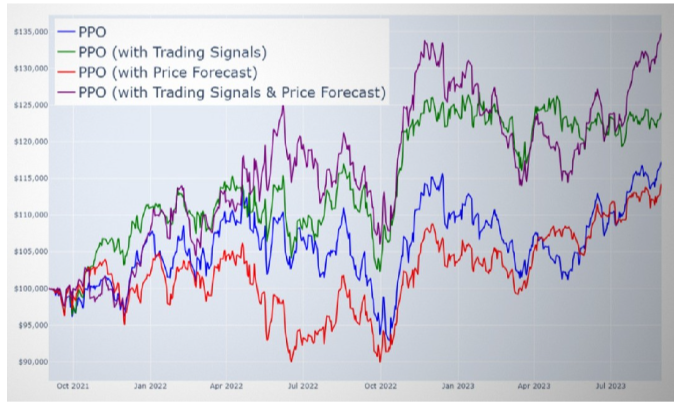
Figure 3: Portfolio value of the Multi-modal DRL Solution

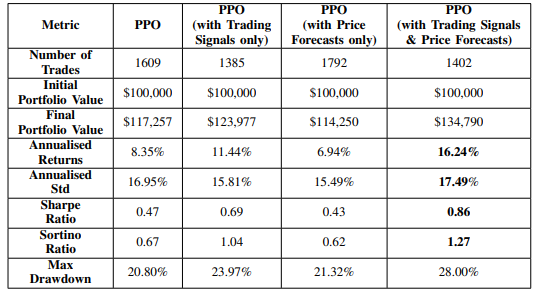
Table 1: Performance of Multi-Modal Solution

As shown in Table I, the Multi-modal DRL solution demon- strates superior performance in risk-adjusted returns.

Comparative Performance Against Benchmarks

The performance of the Multi-modal DRL solution was benchmarked against traditional investment strategies, including:

DJI Index: Represents a buy-and-hold strategy using index funds or ETFs that replicate the Dow Jones Industrial Average (DJI) performance.

• Equal Weightage: Allocates investments evenly across all portfolio stocks, promoting diversification.
• Min-Variance: Employs the mean-variance optimization technique, leveraging the Sequential Least Squares Programming (SLSQP) algorithm to minimize portfolio variance using the past 252 days’ prices.
• Best Stock: Involves buying and holding the bestperforming stock during the training period, identified as Apple Inc. (AAPL).

AS illustrated in Figure 4, the DRL PPO model−enhanced with Algorithmic Trading Signals and LSTM-based Price Fore- casts− demonstrates a clear and consistent outperformance overall benchmark strategies. Table 2 further substantiates this by showing that our model achieves the highest Sharpe Ratio and Sortino Ratio, underscoring its exceptional capacity to optimize returns while effectively managing risk.

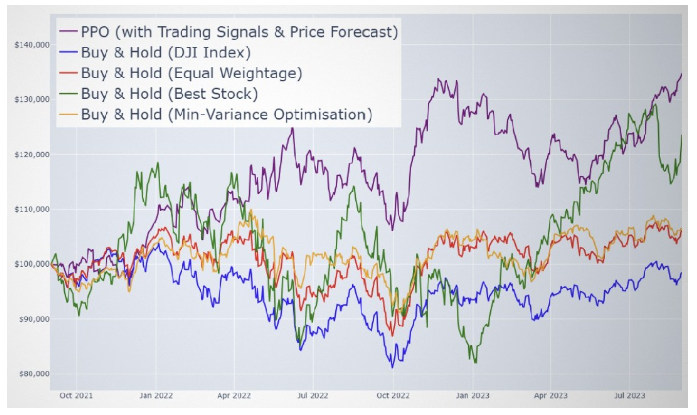
Figure 4: Portfolio Value of Multi-modal DRL Solution Against Benchmarks

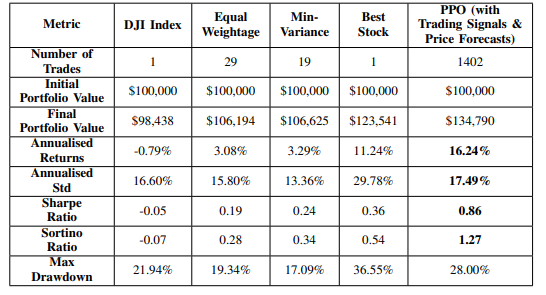
Table 2: Performance of Multi-Modal Solution Against Benchmarks

In terms of annualized returns, the Best Stock bench-mark approached the performance of our model but did so with markedly higher volatility and a significantly greater annualized standard deviation, highlighting the inherent risks of concentrated, singlestock strategies. On the other hand, risk-averse approaches such as Equal Weightage and Minimum Variance yielded lower volatility, yet at the cost of substantially diminished returns.

The proposed multi-modal framework−combining deep reinforcement learning with algorithmic trading signals and LSTM-based price forecasts−demonstrates a well-calibrated trade-off between return and risk. Its consistently superior Sharpe and Sortino Ratios validate its effectiveness in optimizing risk-adjusted returns under dynamic mark et conditions. Theses results confirm the model’s robustness in achieving strong risk-adjusted performance, reliably outperforming conventional benchmarks in both return efficiency and risk control.

Market Regime Stress Testing

The model was evaluated across distinct market regimes, including the 2008 Global Financial Crisis, the 2020 COVID-19 crash, and the 2022 geopolitical tensions. The multimodal framework maintained positive Sharpe and Sortino Ratios, demonstrating adaptability to both bullish and bearish conditions. The use of LSTM forecasts and technical signals contributed to this robustness.

Acknowledgement

We sincerely appreciate the support of National University of Singapore (NUS) in supporting this research. Their insights and resources have been invaluable in advancing our work.

Conclusion

This study introduced a Multi-modal Deep Reinforcement Learning (DRL) solution that integrates Algorithmic Trading Signals and LSTM-based Price Forecasts, demonstrating sub- stantial improvements over traditional benchmarks in terms of risk-adjusted returns. Key results, such as a 16.24% annualized return, 17.49% annualized standard deviation, Sharpe ratio of 0.86, and Sortino ratio of 1.27, highlight the model’s effectiveness in delivering strong profitability while managing risk.
The framework was evaluated in a multi-stock trading environment using 29 out of 30 constituent stocks of the Dow Jones Industrial Average (DJI), showcasing its scalability and adaptability to diverse market conditions. However, it is essential to recognize the non-deterministic nature of DRL models, which may produce variable outcomes depending on different configurations. To ensure model robustness and statistical validity, future work should focus on multiple simulations across various scenarios before deployment in real-world environments.

While the performance results are promising, several lim- itations remain, including the potential for overfitting due to reliance on historical data, the binary nature of trading signals, and the limited action space that restricts more complex trading strategies. Addressing these challenges, along with incorporating alternative data sources and real-world trading constraints, could further improve the framework’s robustness and adaptability.

This research lays a solid foundation for enhancing algorith- mic trading strategies and setting new benchmarks for risk- adjusted performance in financial markets. Moving forward, future research will focus on fine-tuning model parameters, expanding input modalities, and exploring hybrid architectures to further elevate trading performance and mitigate market risks [16-29].

References

1. Demaine, E., Kopinsky, J., & Lynch, J. (2020). Recursed is not recursive: A jarring result. arXiv preprint arXiv:2002.05131.
2. Moody, J., & Saffell, M. (2001). Learning to trade via direct reinforcement. IEEE transactions on neural Networks, 12(4), 875-889.
3. Jiajie, W., & Liu, L. (2025). Portfolio Optimization through a Multi-modal Deep Reinforcement Learning Framework.
4. Fischer, T., & Krauss, C. (2018). Deep learning with long short-term memory networks for financial market predictions. European journal of operational research, 270(2), 654-669.
5. Jiajie, W., & Liu, L. (2025). Portfolio Optimization through a Multi-modal Deep Reinforcement Learning Framework.
6. Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., ... & Hassabis, D. (2015). Human-level control through deep reinforcement learning. nature, 518(7540), 529-533.
7. Wu, X., Chen, H., Wang, J., Troiano, L., Loia, V., & Fujita, H. (2020). Adaptive stock trading strategies with deep reinforcement learning methods. Information Sciences, 538, 142-158.
8. Fujimoto, S., Hoof, H., & Meger, D. (2018, July). Addressing function approximation error in actor-critic methods. In International conference on machine learning (pp. 1587-1596). PMLR.
9. Jiajie, W., & Liu, L. (2025). Portfolio Optimization through a Multi-modal Deep Reinforcement Learning Framework.
10. Haarnoja, T., Zhou, A., Abbeel, P., & Levine, S. (2018, July). Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In International conference on machine learning (pp. 1861-1870). Pmlr.
11. Zhang, Y., Li, X., Wang, J., Chen, H., & Xu, D. (2022). A Deep Rein- forcement Learning Approach for Financial Market Prediction. Journal of Financial Markets, 60, 101245.
12. Lo, A. W. (2004). The adaptive markets hypothesis: Market efficiency from an evolutionary perspective. Journal of Portfolio Management, Forthcoming.
13. Urquhart, A., & McGroarty, F. (2016). Are stock markets really efficient? Evidence of the adaptive market hypothesis. International Review of Financial Analysis, 47, 39-49.
14. Neely, C. J., Weller, P. A., & Ulrich, J. M. (2009). The adaptive markets hypothesis: evidence from the foreign exchange market. Journal of Financial and Quantitative Analysis, 44(2), 467-488.
15. Liu, X. Y., Yang, H., Chen, Q., Zhang, R., Yang, L., Xiao, B., & Wang, C. D. (2020). FinRL: A deep reinforcement learning library for automated stock trading in quantitative finance. arXiv preprint arXiv:2011.09607.
16. Bahoo, S., Cucculelli, M., Goga, X., & Mondolo, J. (2024). Artificial intelligence in Finance: a comprehensive review through bibliometric and content analysis. SN Business & Economics, 4(2), 23.
17. Ernst, D. (2020). An application of deep reinforcement learning to algorithmic trading. arXiv. org.
18. Pricope, T. V. (2021). Deep reinforcement learning in quantitative algorithmic trading: A review. arXiv preprint arXiv:2106.00123.
19. Wu, X., Chen, H., Wang, J., Troiano, L., Loia, V., & Fujita, H. (2020). Adaptive stock trading strategies with deep reinforcement learning methods. Information Sciences, 538, 142-158.
20. Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.
21. Liu, X. Y., Xiong, Z., Zhong, S., Yang, H., & Walid, A. (2018). Practical deep reinforcement learning approach for stock trading. arXiv preprint arXiv:1811.07522.
22. Azhikodan, A. R., Bhat, A. G., & Jadhav, M. V. (2019). Stock trading bot using deep reinforcement learning. In Innovations in Computer Science and Engineering: Proceedings of the Fifth ICICSE 2017 (pp. 41-49). Springer Singapore.
23. Yfinance. (n.d.). PyPI.
24. Gymnasium documentation. (n.d.).
25. Chen, J. (2022, January 31). What is an iceberg order and how do you identify it?. Investopedia.
26. Scipy.signal.argrelextrema - SciPy v1.13.0 Manual. (n.d.).
27. Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780.
28. Briola, A., Turiel, J., Marcaccioli, R., Cauderan, A., & Aste, T. (2021). Deep reinforcement learning for active high frequency trading. arXiv preprint arXiv:2101.07107.
29. Kalidas, A. P., Joshua, C. J., Md, A. Q., Basheer, S., Mohan, S., & Sakri, S. (2023). Deep reinforcement learning for vision-based navigation of UAVs in avoiding stationary and mobile obstacles. Drones, 7(4), 245.