Research Article - (2023) Volume 2, Issue 4
On The Analysis of Physical Properties of Thermointerfaces Based on Hexagonal Boron Nitride Nanostructures for Cooling the Electronic Component Base of Micro-and Nano electronics
Research Article J Electrical Electron Eng, 2023 Volume 2 | Issue 4 | 439-448; DOI: 10.33140/JEEE.02.04.09
D.А. Prokhorov and S.М. Zuev*
MIREA-Russian Technological University, Vernadskogo Avenue, 78, Moscow, 119454, Russia
*Corresponding Author :S.М. Zuev, MIREA-Russian Technological University, Vernadskogo Avenue, 78, Moscow, 119454, Russia.
Submitted: 2023, September 06; Accepted: 2023, October 13; Published: 2023, November 08
Citation: Prokhorov, D. A., Zuev, S. M. (2023). On The Analysis of Physical Properties of Thermointerfaces Based on Hexagonal Boron Nitride Nanostructures for Cooling the Electronic Component Base of Micro- and Nano electronics. J Electrical Electron Eng, 2(4), 439-448.
Abstract
An empirical study of the physical properties (thermal conductivity, thermal diffusivity, and density) of thermophysical interfaces based on a hexagonal boron nitride (h-BN) nanopowder lattice for cooling electronic component bases in micro- and nano-electronics has been conducted. The physical properties were determined using the laser flash method and the relative method. The potential of compressed nanoparticles of hexagonal boron nitride as a thermophysical interface without an adhesive agent has been described. This article also provides a comparison of the physical properties of other thermophysical interfaces that are widely used today.
1. Introduction
A thermal interface is a multi-component substance that facilitates heat transfer mainly through thermal conductivity from the electronic component base of micro- and nanoelectronics to the cooling radiator. The purpose of this study was to assess the effectiveness of utilizing a boron nitride Nano powder thermal interface with a hexagonal crystal lattice (h-BN) for cooling the electronic component base of micro- and Nano electronics.
At present, two different forms of boron nitride, amorphous (α-BN) and crystalline (cubic c-BN, hexagonal h-BN, and dense, hexagonal w-BN), have been widely produced in mass manufacturing. Hexagonal boron nitride (h-BN) is the most stable crystalline form and is characterized by a layered structure with anisotropic thermal conductivity ranging from 200 to 500 W/mK in-plane and up to 30 W/mK out-of-plane [1,2]. The bandgap (Eg) of hexagonal boron nitride varies widely from 3.6 to 7.1 eV allowing it to be considered not only as a thermoelectric interface, but also as a dielectric as opposed to the works of Seungho Yu and Massoud Kavianya which used metals such as gallium, indium and lead as the thermoelectric interface [3,4].
In this study, the physical properties of copper-based thermoelectric interfaces and hexagonal boron nitride Nano powders under different compression pressures and nanopowder forms with different binding agents (glycerin, caponlac, and glass-like lacquer) were compared.
The granulometric composition of the hexagonal boron nitridecopper nanopowder was measured by laser diffraction and polarization-induced differential intensity scanning (PIDS) with a resolution of several tens of nanometers, as opposed to the work of Martin and Kok where the measurement was carried out by dynamic image analysis, in which the size and shape of the particles were determined by two-dimensional projections on images with resolutions of up to several microns [5].
The thermal conductivity and thermal diffusivity were measured using the laser flash method, in which the temperature rise was measured with respect to time using a cadmium-rutheniumtelluride (CRT) infrared detector.
Researchers studied the effectiveness of therminterfaces in the form of thermal pastes based on "L" and hexagonal boron nitride "P" samples, in which glycerin (samples "M" and "N"), capon lacquer (samples "R" and "S"), and glass-like lacquer (samples "O" and "T") were used as binding agents. Table 1 lists all eight therminterface samples in the form of thermal pastes and powders based on "L" and "P" samples, the physical properties of which were studied at a temperature of plus 100°C (the maximum operating temperature of some integrated circuits, such as the central processor of an electronic computer) at a pressure of 1 atmosphere.
| Sample No | Powder type | Binder | Note |
|---|---|---|---|
| L | Cu | absent | |
| P | nano h-BN | absent | |
| M | Sample L | glycerol CAS 56-81-5 (99,78 %) | The ratio of (1 ± 0.05) g of sample R to (2 ± 0.02) ml. binder |
| R | capon lacquer NC-62B | ||
| O | glass-like lacquer P6V20 | ||
| N | Sample P | glycerol CAS 56-81-5 (99,78%) | |
| S | capon lacquer NC-62B | ||
| T | glass-like lacquer P6V20 |
Table 1: Samples of thermal interfaces in the form of thermal pastes based on samples "L" and "P".
The authors did not consider ethanol and a cold sintering catalyst as binders because in the original works when studying powder graphite, they showed lower efficiency than glycerin [6].
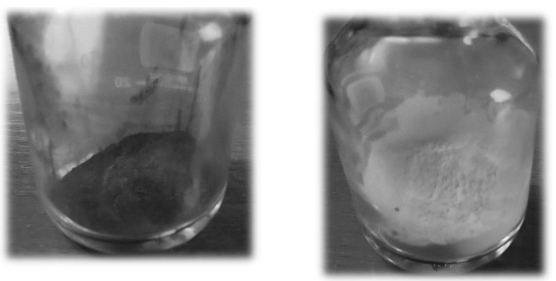
Figure 1: Initial samples "L" (left) and "P" (right).
2. Theoretical Analysis
According to P. Bridgman's theory, which utilizes the method of expressing partial derivatives through the ratio of two expressions rendered by the table separately, determines the thermal conductivity of liquid particles from formula 1 [7].
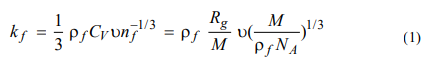
where kf is the thermal conductivity of the liquid, due to molecular interactions, W/m•K; ρf is the density of the liquid, kg/m3; CV is the heat capacity at constant volume, J/kg•K; ʋ - is the sound speed in the liquid, m/s; nf is the particle concentration, 1/m3; Rg is the universal gas constant, J/mol•K; M is the molecular mass, kg/mol; and NA is Avogadro's number, 1/mol.
The ratio of the mass of the original sample to the volume of the binding substance was selected as 1 2 for all samples, based on the practical application of thermal interfaces. However, P [8]. Debaes noted that the viscosity coefficient η of a liquid is sensitive to temperature. At low Reynolds numbers, the viscosity coefficient of the liquid can be determined from the Stokes-Einstein equation 2.

Where η–fluid viscosity, Pa.s; kB–Boltzmann's constant, J/К ;Т–temperature, К; С– constant, in practice accepted 6π or 4π;RS-E is particle radius (m); D is diffusion coefficient (m2/s).
The compressed specimens P and L depicted in Figure 2 are solid bodies for which profiling is necessary in order to solve heat transferal tasks. The main parameters for determining the roughness of the surface are the arithmetic mean of the absolute deviations of the surface from the base plane Ra, the root mean square of the surface heights (RMS) Rq, the mean maximum height of the profile (the mean value of the ten maxima and minima of the surface) Rz, and the maximum height of the surface (the distance between the maximum and minimum of the surface) Rt.
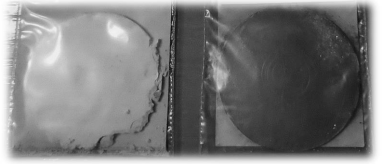
Figure 2: Pressed samples "P" at a pressing pressure of 100 MPa (left) and "L" at a pressing pressure of 300 MPa (right).
With a mathematical approximation for three-dimensional images, Ra is determined using formula 3:
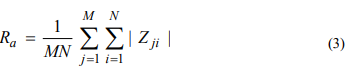
where M and N are the numbers of points in the direction of the abscissa and ordinate, respectively, and Z is the height of the surface relative to the base plane (applicate).
With a mathematical approximation for three-dimensional images, Rq is determined using formula 4:
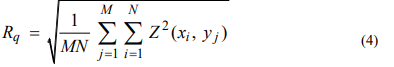
With a mathematical approximation for three-dimensional images, Rz is determined by Equation 5:
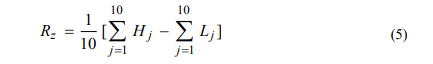
Where Hj is the maximum surface and Lj is the surface minimum. Rt is determined using Equation 6

where Rmax is the surface maximum (distance between the surface maximum and base surface) and Rmin is the minimum surface area (distance between the surface minimum and reference surface).
In solid bodies, the thermal conductivity is determined by the contributions of electrons and quasi-particles, each of which includes the motion of all particles of the crystalline lattice (phonons). The contribution of electrons to the thermal interface coefficient of thermal conductivity can be determined by the Wiedemann-Franz law, based on the Lorenz number obtained by Zommerfeld with the help of quantum statistics, according to Equation 7:

where ke–coefficient of thermal conductivity of a solid, due to interactions between electrons, W/m•К; e – electron charge, С; σ–conductivity, S/m
The contribution of phonons to the thermal conductivity of the thermal interface can be determined using Equation 8.

where Kφ–coefficient of thermal conductivity of a solid, due to interactions between phonons, W/m•К; Λ – phonon mean free path, m; u – average speed of phonon oscillations, m/s; C – specific volumetric heat capacity, J/m3•К
Methodology
Prior to the fabrication of the “P” and “L” specimen-based thermal interfaces, granulometric measurements of their compositions were performed using light diffraction and registration of the differential intensity of the polarized light (PIDS) by the LS 13 320 MW particle laser analyzer. The diffraction-based measurement resulted in the determination of the particle diameter that scattered light, similar to the measured particle of the respective sample. The volume percentage distribution of ‘P’ and ‘L’ specimens according to their diameter is depicted in Figures 3 and 4, respectively. The LS 13 320 MW particle laser analyzer has the scope of measurement corresponding to a particle diameter from 40 nm to 2000 µm.
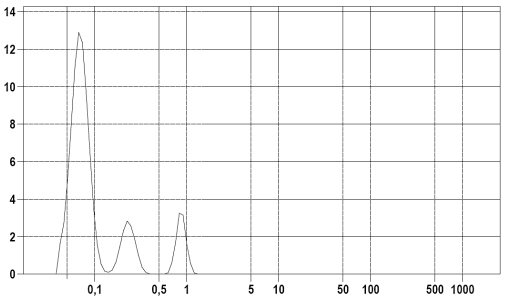
Figure 3: The dependence of the percentage distribution of the volume of particles on their diameter of the sample "P" (specific surface area 72,50 m2/ml).
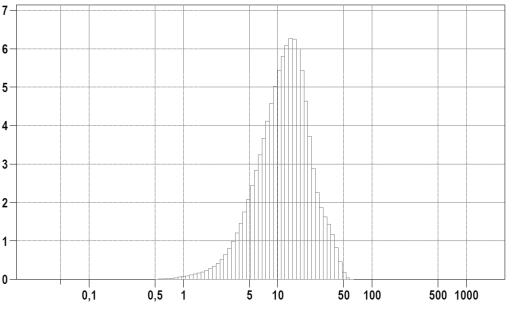
Figure 4: The dependence of the percentage distribution of the volume of particles on their diameter of the sample "L" (specific surface area 0,69 m2/ml).
Samples "L" and "P" were pressed on the vulcanization press fitted with a hydraulic drive, to pressures of 2.3 and 44.13 MPa, respectively. The samples were placed within a silicone plate held to receive the powdered material. After each pressing, additional amounts of powder were added to the form, and the pressing procedure was continued until the final shape was attained, as illustrated in Figure 5.

Figure 5: Appearance of samples “L” pressed to a pressure of 2.3 and 44.13 MPa and samples “P” pressed to a pressure of 2.3 MPa.
Samples "L" and "P" were pressed to a pressure of 300 MPa in an IP-1000 hydraulic press. To prevent the sample "P" from sticking to the punches, hexane (C6H14) was added to moisten it, and to prevent dispersion and provide stability during pressing, ethanol (C2H6O) was added to the sample "L". The press form, with a diameter of 34 mm, used for forming samples "L" and "P" in the pressing process under a load range from 20 to 30 tons, is shown in Figure 6.

Figure 6: Mold with a diameter of 34 mm, used in the formation of samples "L" and "P" in the process of pressing under a load range of 20 to 30 tons.
The binding agent for samples "M" and "N," 99.78% glycerin CAS 56-81-5, was used. As the binding agent for samples "R" and "S," capon lacquer NC-62B was used. As the binding agent for samples "O" and "T," glass-like lacquer P6V20 was used. The mass of samples "L" and "P," used for their creation, was determined by electronic scales and the volume of the binding agent was by pipetting Black DPO-1-1000-10000 one-channel dosing.
The essence of the laser flash method used to measure the thermal conductivity λ and the thermal diffusivity α of the samples with the help of an analyzer for the thermal diffusivity and thermal conductivity LFA 467 Hyper Flash, involves mounting the sample in a calorimeter, the bottom surface of which is heated by pulses of radiant energy of 10 J duration 0.6 ms, created by a xenon lamp. The change in temperature of the calorimeter's top surface was recorded by a cadmium-radium-telluride (MCT) infrared detector. Measurements were made after thermos tatting the samples for 60 minutes at a constant temperature. The interval between pulses (shots) τ was 7 minutes. Laser voltage - 250 V. The number of pulses made was between 7 and 10 to establish the average value of the measured variable. The temperature of the sample can be determined according to formula 9 [9].

The density of the samples ρ was determined after prethermostating at a temperature of plus 100
4. Experimental Part
The roughness of the sample "P" compressed under 300MPa is shown in Figure 7 with different resolutions. Table 2 shows the results of the measurement of the physical properties of the samples by the laser flash method.
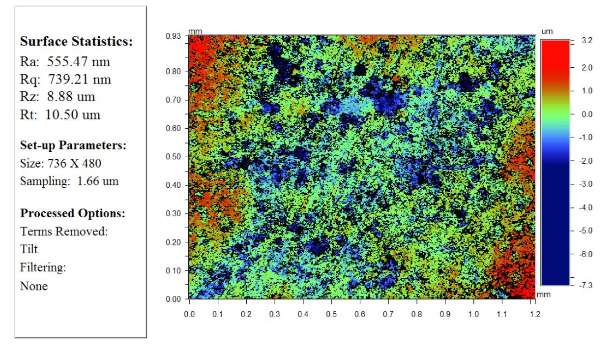
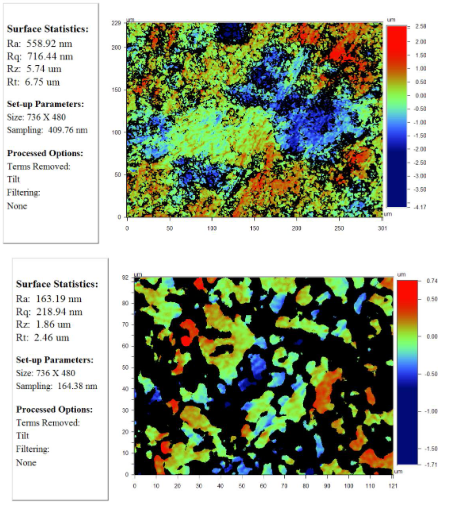
Figure 7: The surface roughness of the sample "P", pressed under a pressure of 300 MPa:
А: increase 5,1x;
B: increase 20,5x;
C: increase 51,1x.
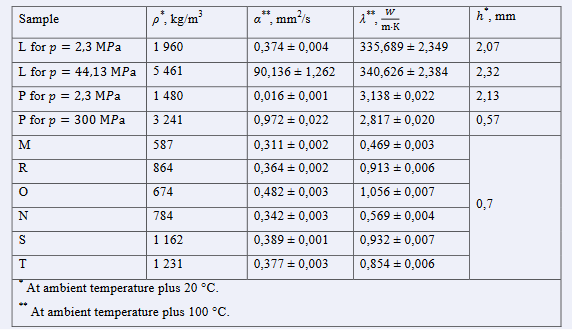
Table 2: Results of measuring the physical properties of samples by the laser flash method
The roughness of the surface of specimen "L" compressed under a pressure of 300 MPa is depicted in Figure 8 with various resolutions.
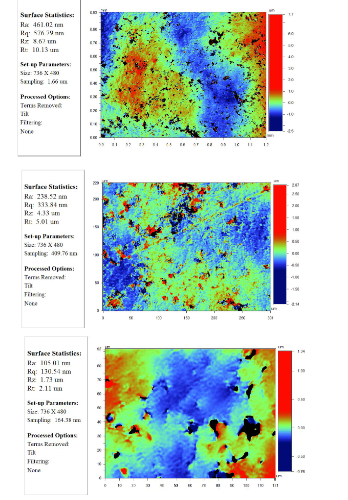
Figure 8: igure 8: The surface roughness of the sample "L", pressed under a pressure of 300 MPa:
А: increase 5,1x;
B: increase 20,5x;
C: increase 51,1x.
5.Results and Its Discussion
The percentage distribution of the particle size from their diameter in samples "P" and "L" (Figure 3, 4) showed that the values of the modal diameters of the investigated boron nitride hexagonal powder and copper powder were 67 nm and 13.6 μm respectively, the average values were 106 nm and 11.3 μm respectively, and the median values were 75 nm and 12.1 μm respectively. The obtained values allow the application of thermal interfaces based on copper and boron nitride hexagonal powder for cooling of micro- and nanoelectronics devices.
High thermal and temperature conductivity values were observed in compressed samples due to their higher density compared to the same samples in original (powder) form. However, upon considering the changes in density and thermal conductivity upon pressing at 2.3 to 300 MPa for sample “P” and 2.3 to 44.13 MPa for sample “L”, it could be seen that pressing of sample “P” increases its density by 2.2 whilst its thermal conductivity slightly decreases by 11%, whereas, when sample “L” is pressed, its density increases nearly 3 times while its thermal conductivity slightly increases by 1.5%. These relations indicate that compression of sample “L” slightly increases its thermal conductivity however this is not the case for sample “P” in which compression leads to a slight decrease in thermal conductivity due to factors beyond increase in density. Two primary factors affecting thermal conductivity in such a case may be particle connectivity and the presence of defects, as average particle diameter for sample “P” is two orders of magnitude lesser than sample “L”, and the investigated boron nitride has a hexagonal crystal lattice whereas copper is presented with cubic. It is supposed that particle connectivity increases the thermal conductivity and temperature conductivity of the sample due to increased phonon free path length, while increase in defect numbers reduces thermal conductivity by restricting it.
In the case of creating a thermo-interface in the form of thermopast, the most promising appears to be the use of glass- like lacquer as the binding substance for the "L" sample, and capon lacquer for the "P" sample, instead of glycerin, since the thermal conductivity coefficient for the "O" and "S" samples respectively is approximately 2 times higher.
In the case of creating a thermo-interface in the form of thermopast, the most promising appears to be the use of glass- like lacquer as the binding substance for the "L" sample, and capon lacquer for the "P" sample, instead of glycerin, since the thermal conductivity coefficient for the "O" and "S" samples respectively is approximately 2 times higher.
6. Conclusion
Thus, in this work, the physical properties of thermointerfaces were determined empirically based on powdery copper and nanobeads of hexagonal boron nitride with different particle sizes, which allowed the determination of their fundamental differences during compaction.
Despite its higher thermal conductivity, the practical efficiency of using a copper-based thermal interface in the form of thermal paste to cool integrated circuits is virtually equivalent to that of a hexagonal boron nitride nanoparticle-based thermal interface. The smaller particle size of hexagonal boron nitride nanoparticles relative to the copper-based powder leads to significantly less roughness in the surface of the thermal interface in the form of a pressed thin film, which in practice will allow for a greater area of contact with the cooled surface.
It is suggested that increasing the thermal conductivity and temperature conductivity of hexagonal boron nitride nanowires could be further examined by looking into its planar physical properties at the same pressures while imposing one orientation for the majority of its particles as, in the present study, only its out-of-plane physical properties at a random particle orientation were addressed.
The measurement of the roughness of the compressed samples based on copper and hexagonal boron nitride shall permit their consideration for practical thermal transfer calculations.
Conflict of Interest
The authors declare that they have no conflict of interest. The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Funding
The work was performed using the equipment of the Shared Use Center (CCU) of the Russian Technological University (RTUMIREA) with the support of the Russian Ministry of Education and Science.
The study was supported by the Russian Science Foundation grant No. 23-29-00079, https://rscf.ru/project/23-29-00079
References
- Liu, D., Chen, X., Yan, Y., Zhang, Z., Jin, Z., Yi, K., & Wei,D. (2019). Conformal hexagonal-boron nitride dielectric interface for tungsten diselenide devices with improved mobility and thermal dissipation. Nature communications, 10(1), 1188.
- Sarkarat, M., Lanagan, M., Ghosh, D., Lottes, A., Budd, K., & Rajagopalan, R. (2020). Improved thermal conductivity and AC dielectric breakdown strength of silicone rubber/BN composites. Composites Part C: Open Access, 2, 100023.
- Solozhenko, V. L., Lazarenko, A. G., Petitet, J. P., & Kanaev, A. V. (2001). Bandgap energy of graphite-like hexagonal boron nitride. Journal of Physics and Chemistry of Solids, 62(7), 1331-1334.
- Yu, S., & Kaviany, M. (2014). Electrical, thermal, and species transport properties of liquid eutectic Ga-In and Ga- In-Sn from first principles. The Journal of chemical physics, 140(6).
- Martin, R. L., & Kok, J. F. (2017). Wind-invariant saltation heights imply linear scaling of aeolian saltation flux with shear stress. Science advances, 3(6), e1602569.
- Prokhorov, D. А., & Zuev, S. М. (2023). On the Analysis of Physical Properties of Thermointerfaces Based on Hexagonal Boron Nitride Nanostructures for Cooling the Electronic Component Base of Micro-and Nanoelectronics.
- Yu, S., & Kaviany, M. (2014). Electrical, thermal, and species transport properties of liquid eutectic Ga-In and Ga-In-Sn from first principles. The Journal of chemical physics, 140(6).
- Datta, J., & Majumder, C. (2023). Entrapping metal atom on hexagonal boron nitride monolayer for high performance single-atom-catalyst: Role of vacancy defects and metal support. Applied Surface Science, 614, 156061.
- Xie, H., Cai, A., & Wang, X. (2007). Thermal diffusivity and conductivity of multiwalled carbon nanotube arrays. Physics Letters A, 369(1-2), 120-123.
- Monezi, C. A., Grigorov, K. G., Tsanev, A., Godoy Jr,A., Couto, A. A., Lima, A. O., ... & Massi, M. (2022).Synthesis and Characterization of Nanocrystalline Boron- Nitride Thin Films by Ion Milling and Thermal Treatment for Tribological Coatings: An Approach to Quantifying the Growth Dynamic Process. Materials, 15(5), 1761.
Copyright:
Copyright: ©2023 S.М. Zuev, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.