Heat Integration as a Strategic Economic Basic Ingredient for Viable Clean Technologies: Perspective of Return on Incremental Investment

Introduction

The integration of renewable energy sources with industrial processes can be exemplified by the running research on using solar energy to run a heat pump to raise the temperature of a distillation column overhead distillate, which can then be used, to comply with the second law of thermodynamics, to supply heat to the distillation column bottoms.

The distillate contains energy at a lower temperature than the distillation bottoms. By integrating the heat from the solar energy into the distillate, the temperature of the distillate is increased, allowing for the transfer of heat to the bottoms stream, making use of the temperature gradient, to comply with the second law of thermodynamics.

Implementing this heat integration strategy, the process can reduce its reliance on conventional fossil-based fuels and utilize renewable energy sources, leading to energy savings and reduced environmental impact. Another example of integrating renewable energy with traditional energy applications has been recently published by Bipongo et al. for a hybrid micro-grid system using renewable energy [1].

Heat integration in industry plays a crucial role in mitigating climate change by reducing energy consumption, fossil fuel  consumption, and greenhouse gas emissions.

The escalating apprehension regarding climate change mitigation has intensified the search for reducing industrial energy consumption and at the same time the quest for alternative sustainable economically viable energy sources. Within the context, the carbon-intensive chemical and refinery industries are glaring examples of where future research efforts should be targeted. Distillation columns in the chemical industries for example are reported to consume 40% to 60% of total US manufacturing industry energy usage and 6% of total US energy consumption. The concept of sustainable development is now accepted as a means of protecting the environment. Nonetheless, most of the research thrust in the past decades was focussed, understandably, on technical innovations and the search for available-on demand alternatives rather than the economic viability of the proposed process.

There is scarcity in the literature on the economic techniques for rigorous economic analysis for the evaluation of emerging energy efficient technologies. Any new technology must be economically viable to be accepted and commercialized as an energy source to meet market demand.

For green grass projects, the design stage should involve the consideration of the economics of heat integration. The ensuing capital costs associated with the addition of such equipment for the purpose of reducing external utility operating costs must realize an acceptable return on investment. Capital costs and operating costs are in essence contradictory targets, which should be resolved by applying optimization studies.

In this study, the novel concept of Return on Incremental Investment (ROII) is presented. The basic idea is that when considering an energy-saving technology that involves capital expenditure, such as proposing new and more efficient equipment as an alternative or replacement for less efficient equipment, it is imperative to ensure the economic viability of this investment by evaluating the resulting energy savings. The ROII Metric is defined as the percentage of the ratio of annual savings in energy to the ensuing increase in capital expenditure in terms of depreciation cost of equipment. The technique is applied to a case study.

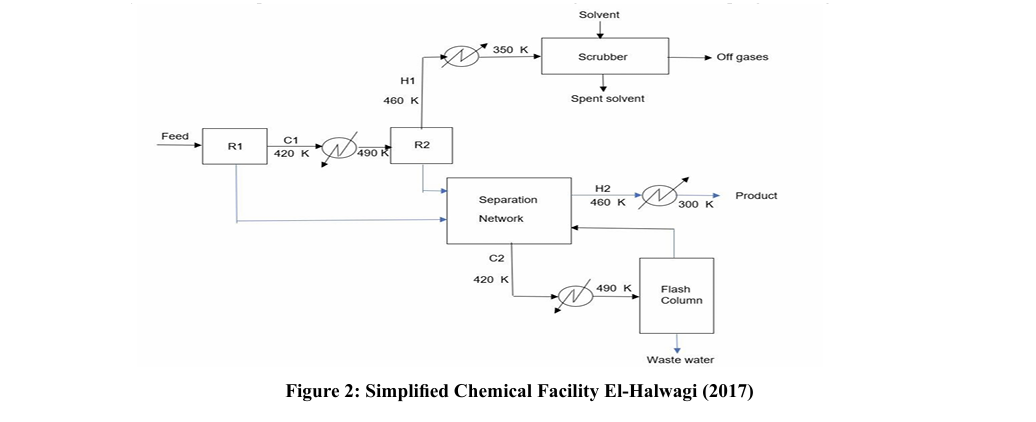
The case study outlined in this study is the chemical processing facility shown in Figure . 2 below adapted from El Halwagi [2]. The process involves two adiabatic reactors, a scrubber, a separation network, two heaters, two coolers, and a flash column.

In this contribution, a step-by-step procedure is outlined from conception to the final calculation of ROII. The algebraic method was used to determine the location of the pinch point(s) and the minimum heating and cooling duties. The synthesis of the optimized HEN was then determined using the LINGO linear programming software.

The breakthrough of the concept of pinch technology in optimal HEN design was introduced by Linnhoff and Flower and Linnhoff and Hindmarsh. Since its introduction, pinch technology has been extensively applied in engineering and other fields.
The pioneering work of El-Halwagi and Manousiouthakis and El-Halwagi saw the introduction of mass exchange networks to parallel the concepts of HENs. Considerable research was carried out on the problem of reducing the usage of external sources of heating and/or cooling utilities (Yong 2023) [6-12]. Several reviews were published on the subject (Manan 2016). HENs enhance sustainability of fuel resources by optimizing energy usage within industrial processes. This can contribute to a more sustainable and efficient use of available fuel resources. Furthermore, recovering and reusing waste heat reduces plant operating expenses by reducing the need for additional fresh energy inputs.

In pinch technology, the entire process is conceived as a wholesome entity and the targeting of minimum heating and cooling requirements are established prior to the detailed design calculations.

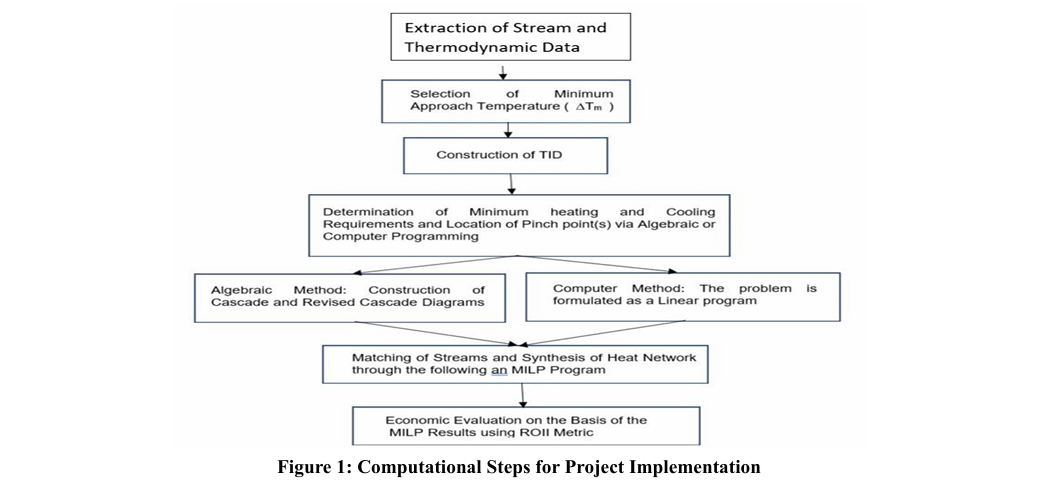
The next step is the sustainable design stage where synthesis of the HEN with the optimum matching of the hot and cold streams to realize the targets obtained in the first stage. The synthesis task can be accomplished through manual, flow sheeting, or computer commercial software El-Halwagi. Figure.1 shows the general outlines of the computational steps in optimal HEN design.

The main task in network synthesis is determining the minimum number of heat exchangers, which would achieve the minimum utility targets set in the targeting stage. It is implicitly assumed here that the minimum number of heat exchangers is tantamount to minimum capital cost.

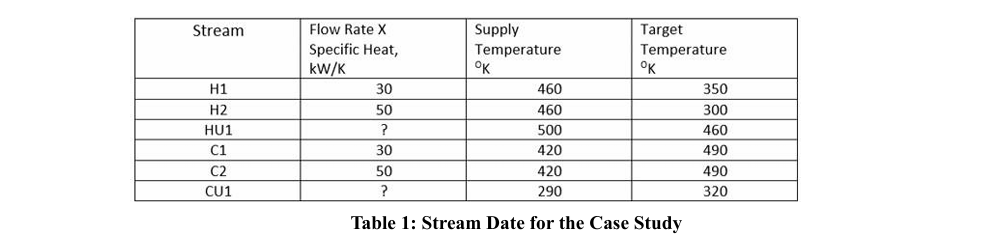
The stream data for the simplified chemical facility is given TABLE 1 below.

The first step in the analysis involves the determination of the location of the pinch point(s) and the ensuing heat integration subnet works El-Halwagi [2]. The temperature interval diagram (TID) is shown in TABLE 2 below.

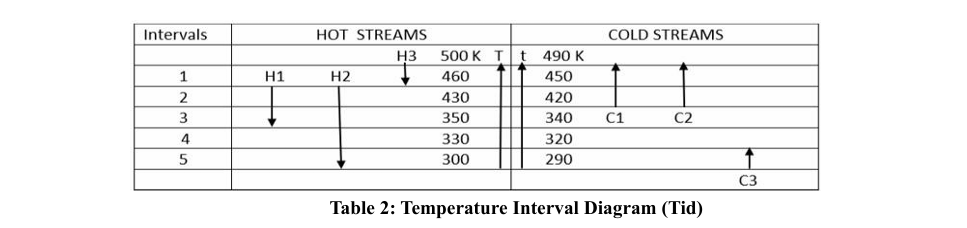
Flow rate x Specific heat for streams H1, H2, C1, and C2 are 30, 50, 30, and 50 kW/K respectively. Figure 3 and Figure 4 show the cascade and the revised cascade diagrams.

The revised cascade diagram shows that there are two zero heat residuals, which results in three heat subnetworks. The revised cascade diagram also indicates that the minimum heating requirements are 3200 kW and the minimum cooling requirements are 8900 kW. The locations of the three subnetworks are shown in TABLE 3 below. The revised cascade diagram shows that there are two zero heat residuals which results in three heat subnetworks. The revised cascade diagram also indicates that the minimum

Stream matching is implemented within each subnetwork separately to avoid cross matching over pinch borders. Matching of streams across pinch line would result in passing heat through a pinch, which would result in three negative results:

• Increasing heating requirements
• Increasing cooling requirements
• Reducing heat exchange in the overlapping heat exchange range

Stream matching of each couple of streams involves the determination of the upper limit of heat exchange between the heat load of the hot stream and the capacity of the cold stream according to the constraint relationship ElHalwagi.

The optimization stage in this study involves the determination of the minimum capital cost that meets the minimum operating costs already realized in the algebraic method through the revised cascade diagram.

The total number of heat exchangers is the sum of all possible matching of streams in the three subnetworks. The symbol Eij is used to refer to the heat exchanger which exchanges heat between hot stream (i) and cold stream (j). The objective function to be minimized is thus:

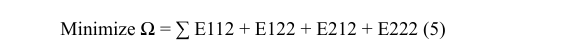
The software LINGO is used to run the linear programming optimization program. The following table includes the required data for program execution. Stream matchings are implemented within individual subnetworks only. In each stream, matching the upper bound of the heat stream load and the cold stream capacity is taken as the exchangeable load. The table of exchangeable heat loads is shown in Table 4 below.

In addition to the objective function equation, the LINGO program involves heat balances for H1, heat balances for H2, heat balance for HU (H3), heat balances for C1, heat balances for C2, heat balance for CU (C3), matching of loads equations, non-negativity constraints, and declaration of binary integers El-Halwagi.

The solution of the LINGO program indicates that the optimal configuration network requires the introduction of two heat exchangers out of the possible four cases in the objective function. In addition, two smaller heaters and two smaller coolers are needed to provide the utility loads needed to meet the minimum requirements specified in the revised cascade diagram. Figure 5 below shows the expedient placement of the two heat exchangers E112 and E122 and the smaller two heaters and two coolers in the integrated system.

Results and Discussion

In the economic analysis, the major task is the estimation of the critical costs of the heat exchangers, heaters, and coolers. In making these cost estimates, it is taken into account that heat exchangers are complex devices that are designed to efficiently transfer heat between two completely separated fluids. The heat exchanger purchased cost is affected by many factors such as exchanger type, fluid characteristics, design specifications, materials of construction, operating conditions, manufacturing flexibility, suppliers and market conditions, and quantities purchased. In addition, heat exchangers may have additional features such as fins, tubes, or plates to enhance heat transfer, which can further increase their cost. Furthermore, the assumed overall heat transfer coefficient impacts heat transfer area, thus size, and cost of equipment. On the other hand, heaters and coolers are typically simpler in design and construction. They may consist of basic components such as heating elements or cooling coils, which are relatively less expensive, compared to the complex configuration of heat exchangers. For these considerations, the cost of a heater exchanger is a multiple of the cost of a heater or cooler of the same size and material of construction. In this study, it was estimated the cost of a heat exchanger would be a double multiple of a heater or cooler.

The implementation of the new network to replace the heating and cooling equipment entails expenditure of capital. This capital cost must be economically justified by the savings in utility costs. The annual net profit is the discrepancy between the sum of the original utility costs plus the annualized capital cost of the heaters and coolers and the sum in the integrated case of the new utility costs plus the annualized capital cost of the introduced heat exchangers and any remaining heaters and coolers, if any. The realized annual profits must be sufficiently high to justify the new investment. Benchmarking of the optimized HEN performance can be assessed through the return on incremental investment criterion (ROII).

The ROII is calculated as follows:

The base case investment = Purchased costs of base case two heaters and two coolers.

The integrated case investment = Purchased costs of two heat exchangers + Purchased costs of the new two heaters and two coolers.

Incremental capital investment = Integrated case capital investment – Base case capital investment

Annual Profits = Annual savings in utility costs + annual savings in depreciations costs (which are expected to be negative in value) ROII = Annual profits / Incremental capital investment Utility costs for the two cases were calculated on the basis of cooling water cost at 0.354 ($/GJ) and steam cost at 6.08 ($/GJ). Annual cooling water cost for cooling of streams H1 and H2 = (3,300 + 8000) X 10-6 GW X 3600 X 7920 s/yr X 0.354 $/GJ = Annual steam cost for heating of streams C1 and C2 = (2,100 + 3500) X 10-6 GW X 3600 X 7920 s/yr X 6.08 $/GJ The utility costs for the base case are shown in TABLE 5 below.

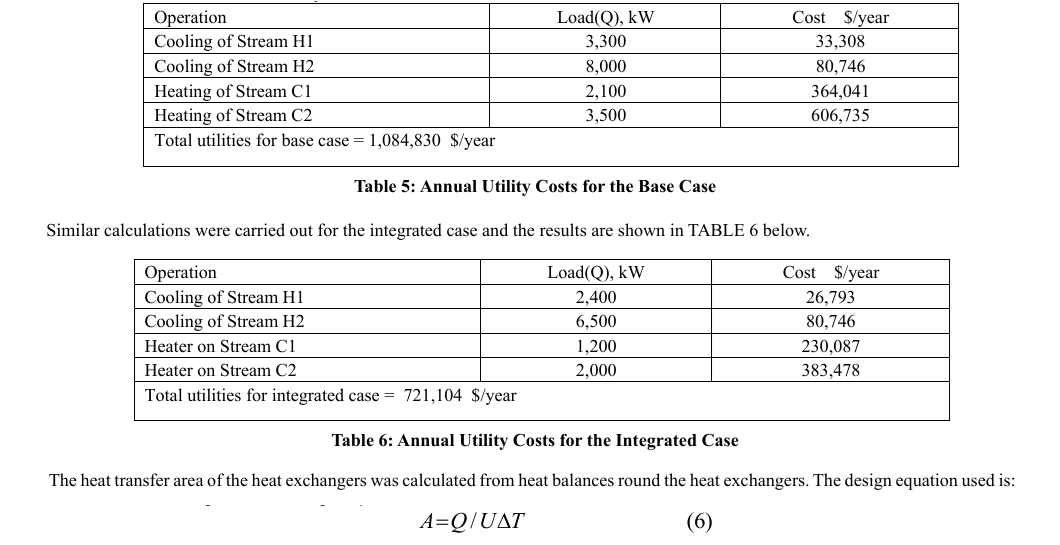
Where Q is the heat load, U the overall heat transfer coefficient, and ΔT is the temperature difference between the hot and cold fluids. The individual heat temperate difference above ΔT is used rather than the log mean temperature difference (LMTD) because the log mean temperature difference is usually used in heat exchanger design, analysis, and measurement of heat exchanger performance. The difference in accuracy between the two methods might be negligible when the temperature differences are small or when the fluids are nearly counter-current.

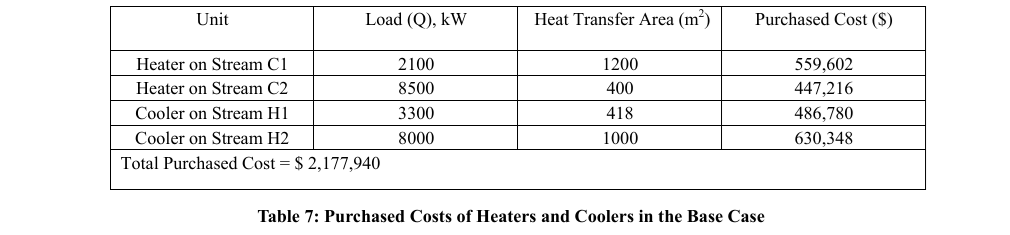
The installed cost of each heat exchanger was estimated on the basis of $500 per square meter. The installed costs of the coolers and heaters were estimated as 50% of the cost of a comparable heat exchanger with the same heat transfer area and material of construction. Then the difference in costs due to sizes was corrected using the six-tenths rule. The material of construction is carbon steel for all equipment. The purchased costs of heaters and coolers in the base case are shown in TABLE 7 below.

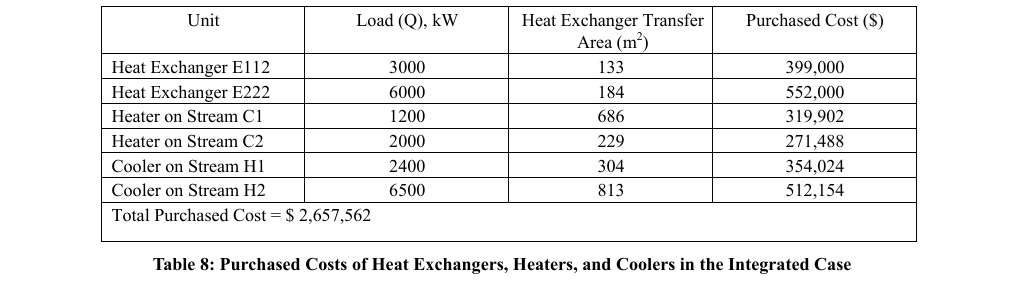
The purchased costs of heat exchangers, heaters, and coolers in the integrated case is shown in TABLE 8 below. Equipment life time of 10 years is assumed for the calculation of depreciation costs.

Depreciation costs of equipment for the base case = 2,177,940/10 = 217,794 $/year
Total of utilities and equipment depreciation costs for base case = 1,302,624 $/year
Depreciation costs of equipment for integrated case = 2,657,562/10 = 265,756 $/year
Total cost of utilities and equipment depreciation costs for integrated case = 986,860 $/year
Net annual savings in utility and equipment depreciation costs = 1,302,624 - 986,860 = 315,764 $/year
Incremental capital = 2,657,562 - 2,177,940 = $ 479,937
Percentage return on incremental capital cost (ROII) = (315,764/479,622)*100 = 65.8%

Sensitivity Analysis

Fuel cost have a sginificant impact on process econmic performance in general and on thermal process integration in particular. Table 9 below shows the sensitivity of changes in utilities' costs (which are directly driven by fuel costs) on annual profits. An increase in utilities costs represents an increase in both versions of the projects under study and thus represent an increase in the difference of the utility costs between the two cases. In other words, an increase in utility costs improves the value of the ROII. For example, a 10% increase in utility costs would be reflected in a 10% increase in annual savings. The results of the calculations are as follows:

Net annual savings in utility and equipment depreciation costs = 315,764 $/year
Annual savings in utility costs alone = 1,084,830 - 721,104 = 363,726 $/year
Net cost in depreciation costs = 72,598 - 181,700 = -47,962 $/year

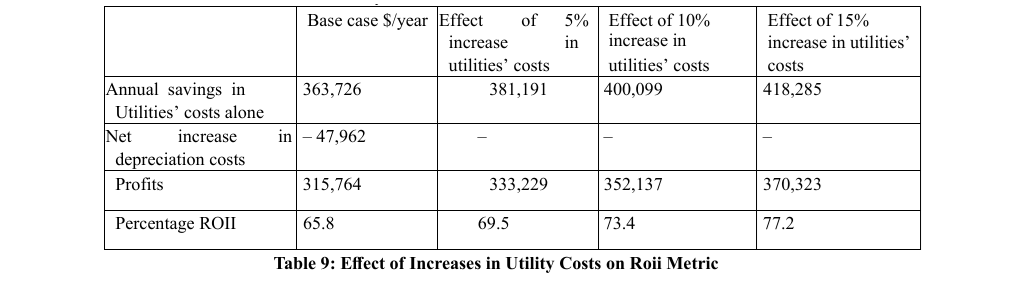
Table 9 above indicates that the profitability of the proposed integration in terms of the ROII metric is very sensitive to increases in utility costs, which are directly impacted, by increases in energy costs.

On the other hand, a decrease in energy costs reduces utility costs and subsequently the difference between the utility costs of the two cases under consideration. Such a situation reduces the economic incentive to implement thermal integration. Table 10 below of lower utility costs on process economic performance. assesses the effect of lower utility costs on process economic performance.

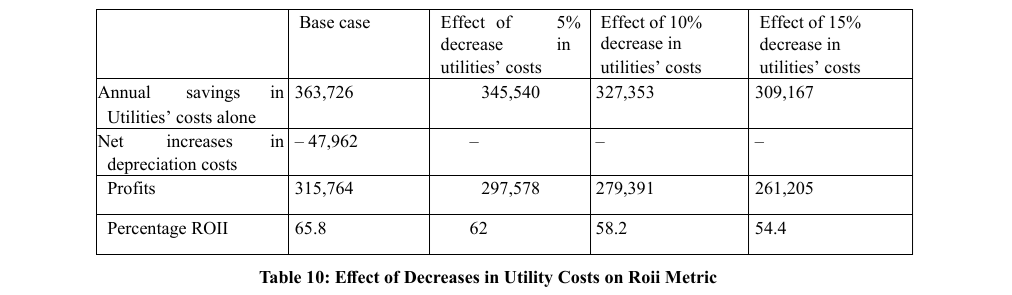
Table 10 indicates that there is an important threshold of minimum or cut off ROII (to be predetermined by plant manager) below which the project becomes economically untenable. Throughout the sensitivity analysis it is assumed that the equipment costs remain constant and do not fluctuate as does the utility costs.

Conclusions

The results of the study highlight the sensitivity of profits to utility costs, which are driven directly by energy costs fluctuations. The impact of changes in capital costs also impact profitability but to a lesser extent because these effects are delayed and are not immediate. The estimation of equipment costs is critical to the assessment of project economic performance. The economic viability is highly impacted by the cost of heat transfer equipment in terms of dollars per unit surface area as quoted from market suppliers. The equipment heat transfer area is critically sensitive to the assumed overall hear transfer coefficient (U). The cost of heat exchangers, heaters, and coolers should be obtained directly as quotations from manufacturers or vendors. The project realizes a ROII of 65.8%. The steps outlined in this contribution would assist decision makers and researchers in arriving at logical actions based on informed opinions.

Statements and Declarations

Funding

The authors declare that no funds, grants, or other support were received during the preparation of this manuscript

Competing Interests

The authors have no competing interests to declare that are relevant to the content of this article. All authors certify that they have no affiliation with or involvement in any organization or entity with any financial interest in the subject matter or materials discussed in this manuscript. The authors have no financial or proprietary interests in any material discussed in this article.

Data Availability Declaration

The authors declare that any data supporting the findings in this study are available within the paper.

References

1. Ndeke, C. B., Adonis, M., & Almaktoof, A. (2024). Energy management strategy for a hybrid micro-grid system using renewable energy. Discover Energy, 4(1), 1.
2. El-Halwagi, M. M. (2017). Sustainable design through process integration: fundamentals and applications to industrial pollution prevention, resource conservation, and profitability enhancement. Butterworth-Heinemann.
3. Linnhoff, B., & Flower, J. R. (1978). Synthesis of heat exchanger networks: I. Systematic generation of energy optimal networks. AIChE journal, 24(4), 633-642.
4. Linnhoff, B., & Hindmarsh, E. (1983). The pinch design method for heat exchanger networks. chemical engineering science, 38(5), 745-763.
5. El-Halwagi, M. M., & Manousiouthakis, V. (1989). Synthesis of mass exchange networks. AIChE Journal, 35(8), 1233- 1244.
6. Klemes, J. K., & Wan, Alwi. S. R. (2011). Review of Progress in Integration Technologies for Intensified and Sustainable Processes. Chemical Engineering Research and Design, 89(8), 1271-1288.
7. Klemes, J. J., & Varbanov, P. S. (2012). Process Integration of Heat and Power Systems: A review. Applied Energy, 92(1), 297-313.
8. Jiri, Jaromir. Klemes., Peter, Saber. Vanbnov., Zdravko, Kravanja. (2013). Recent Development in Process Integration. Chemical Engineering Research and Design.
9. Klemes, J.J., & Pierucci, S. (2016) Sustainability Assessment of Process Integration: A review, Journal of Cleaner Production, 133, 38-55.
10. Klemes, J. J., Wang, Q., Varbanov, P. S., Zeng, M., Chin,.H., et al. (2020). Heat Transfer Enhancement, Intensification and Optimization in Heat Exchanger Network Retrofitting and Operation". Renewable and Sustainable Energy Reviews, 120(70), 109644.
11. Wagialla, K. M., El-Halwagi, M. M., & Ponce-Ortega, J. M. (2012). An integrated approach to the optimization of in-plant wastewater interception with mass and property constraints. Clean Technologies and Environmental Policy, 14, 257-265.
12. Wagialla, K. M. (2012). Pinch-based and disjunctive optimization for process integration of wastewater interception with mass and property constraints. Clean Technologies and Environmental Policy, 14, 597-608.
13. Manan, Z. A., Mustafa, s., Shamsuddin, A. H., & Wan, Alwi. S. R. (2016). Energy Integration and Optimization of Industrial Processes Through Pinch Analysis: A Comprehensive Review. Energy Conversion and Management, 105, 821-842.
14. Riadi, I., Putra, Z. A., & Cahyono, H. (2021). Thermal integration analysis and improved configuration for multiple effect evaporator system based on pinch analysis. Reaktor, 21(2), 74-93.