Continual Learning in Machine Intelligence: A Comparative Analysis of Model Performance

Introduction

The field of artificial intelligence is characterized by swift changes and the ongoing introduction of fresh data, requiring models that are not just precise but also capable of adjusting to new conditions as they arise. Building upon the preliminary insights into the concept of continual learning-defined as the capacity of a system to sequentially assimilate new tasks while preserving knowledge from preceding tasks-this manuscript extends the discourse to underscore the paramount importance of continual learning within the domain of artificial intelligence (AI) [1,2]. Termed alternatively as lifelong or incremental learning, continual learning stands at the core of crafting AI systems that are adept in navigating the complexities of dynamic and evolving operational landscapes [3]. These landscapes are marked by variable data distributions, the advent of novel tasks, and the gradual obsolescence of older tasks, compelling a model’s necessity to learn and adapt continuously without necessitating a reinitialization at every juncture of change [4-6]. The exposition delineates the criticality of continual learning in surmounting the constraints posed by static learning frameworks, particularly highlighting the phenomenon of catastrophic forgetting, where the assimilation of new information could inadvertently obliterate previously acquired knowledge [7]. By innovating algorithms and methodologies that seamlessly amalgamate new data while retaining antecedent learning, continual learning endeavors to ameliorate this pivotal challenge, thereby ensuring the sustained efficacy and relevance of AI systems over time [8,9].

Amidst escalating interest from the academic and industrial spheres in continual learning, spanning diverse AI domains such as computer vision, natural language processing, robotics, and autonomous systems, this burgeoning fascination is propelled by the urgent need for AI systems that autonomously refine and enhance their operational performance over time, obviating the need for manual retraining or human supervision [10-12]. This scholarly endeavor seeks to delve into the foundational principles, prevailing challenges, and current progress within the ambit of continual learning, with a focused lens on the pragmatic application and scrutiny of various machine learning models and techniques [13]. By critically evaluating how different algorithms navigate the nuances of continual learning tasks, their manuscript endeavors to shed light on the efficacy and robustness of each model [14,15]. Through this analytical journey, they aspire to furnish the academic community and industry practitioners with profound insights and guidelines, aimed at optimizing AI systems for the demanding requisites of real-world applications, thereby imbuing them with enhanced adaptability, efficiency, and the capability for sustained learning and evolution [16]. Based on existing studies and surveys, it's evident that much of the research conducted thus far has focused on theoretical methodologies and their implementation, the application of continual graph learning and ensemble techniques, an analysis of continual learning leveraging pre-trained models, and investigations into continual learning via neural networks [17-23]. Our investigation contrasts the efficacy of various machine learning models within the context of continual learning, examining how they perform with both initial and subsequent data increments. Furthermore, our evaluation includes an analysis of Mean Squared Error (MSE) and R squared error metrics, which serve as critical benchmarks for assessing the effectiveness of these learning approaches [24].

According to a study conducted by Wang et al., continual learning aims to strike an effective balance between stability and adaptability, thereby ensuring the efficient transfer and application of knowledge to novel tasks [25]. Their study explores various methodologies to assess their suitability in continual learning scenarios, evaluating their effectiveness in addressing real-world challenges. While numerous continual learning (CL) strategies have been suggested by many researchers. For example, Kim and colleagues have not extensively explored the theoretical basis required to effectively tackle the class-incremental learning (CIL) problem. Furthermore, they categorize the CIL challenge into two distinct aspects: forecasting outcomes within individual tasks (Within-Task Prediction, WTP) and identifying the specific task being addressed (Task Prediction, TP) [26]. They also establish a link between task prediction and the capability to detect anomalies or out-of-distribution (OOD) data. A key finding of their research is that the explicit distinction between WTP, TP, and OOD detection is not as crucial as the algorithm’s proficiency in handling WTP and TP or OOD detection, which is vital for achieving optimal performance in CIL settings. Similarly, Jae Seung Kim and colleagues introduce a framework called DASS, which integrates methods designed to address both sudden and gradual shifts in stock data [27]. This framework employs graph learning to analyze temporal and relational dependencies through low-level, relational, and high-level temporal modeling. DASS further enhances its analytical capabilities by incorporating both simple graphs and hypergraphs. Additionally, Da-Wei Zhou and colleagues delve into recent advancements in continual learning using pre-trained models (PTMs) [28]. They categorize existing methods into three distinct groups, discussing their similarities, differences, and the respective advantages and disadvantages.

Moreover, they conduct a practical analysis of leading methods to ensure fairness in these evaluations. Furthermore, Awasthi et al. Explore challenges within the realm of continual learning and critically review contemporary research in the field [29]. They discuss strategies such as parameter regularization to mitigate forgetting in neural networks, the use of memory-based techniques, and the benefits of employing generative models. Additionally, they examine the role of dynamic neural networks in continual learning and suggest directions for future research. In their extensive analysis, German I. Parisi and colleagues identify key challenges associated with lifelong learning in artificial systems and evaluate various neural network strategies that effectively reduce catastrophic forgetting to varying degrees [30]. In the study conducted by V. Khan et al., generative replay is enhanced within a continual learning framework to yield superior performance in challenging scenarios [31]. The team introduces a novel technique whereby generations are cycled through an already trained model to produce reconstructions that more accurately reflect the original data. This method is grounded in the observation that faithful reconstructions are more effective at preserving knowledge. In several instances, this approach demonstrates an improvement over previous generative replay methods.

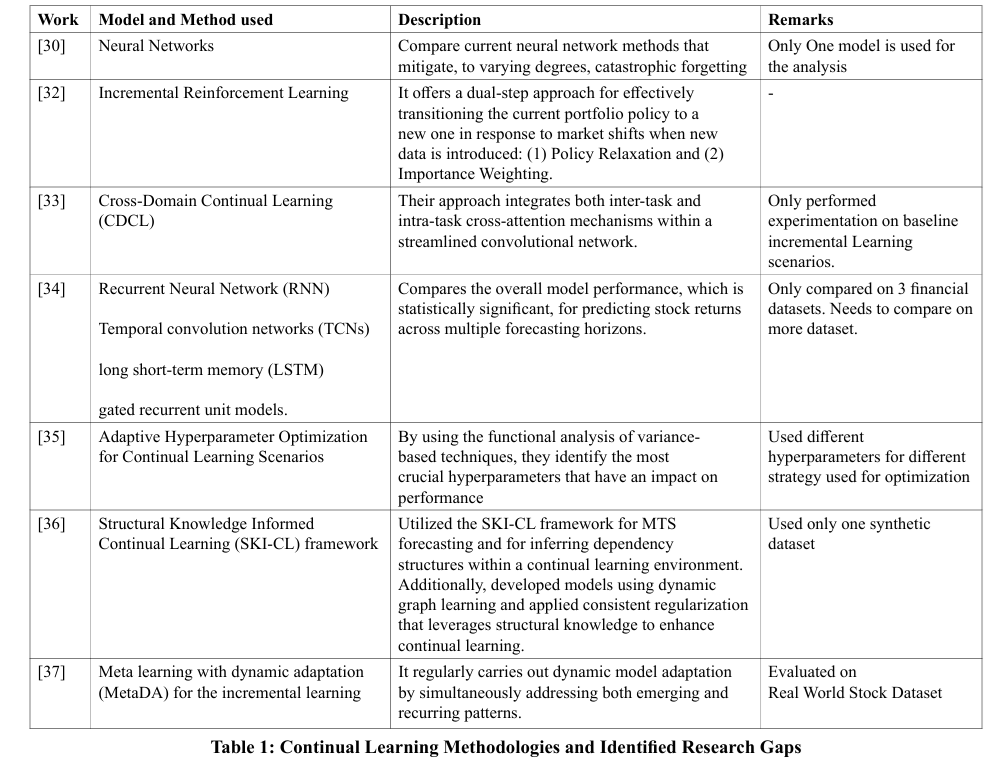
The flow chart of the current research is illustrated in Figure 1, while the available research and detailed survey results of the reviewed papers are presented in Table 1. The surveyed research highlights various methods addressing the challenges of continual learning, with a particular focus on preventing catastrophic forgetting and adapting to changing data environments. Neural networks are recognized for their ability to minimize forgetting, while incremental reinforcement learning offers new strategies to adapt to shifts in dynamic markets. Techniques such as Cross Domain Continual Learning (CDCL) and several recurrent neural network models have shown promise in certain contexts, although they still require extensive validation. Strategies like Adaptive Hyperparameter Optimization and the Structural Knowledge Informed Continual Learning (SKI-CL) framework underscore the significance of parameter adjustments and structural insights in continual learning. However, their effectiveness across different datasets remains to be thoroughly evaluated. Collectively, these studies provide important contributions to continual learning, proposing adaptable and robust solutions necessary for practical use but also highlighting the need for more empirical research to confirm their effectiveness in varied applications.

This study sets itself apart from previous work by offering an exhaustive comparison of multiple machine learning algorithms tailored to continual learning tasks. In particular, this research concentrates on analyzing the performance of eight distinct algorithms—Decision Tree, Ridge, Lasso, Elastic Net, Random Forest, SVR, Gradient Boosting, and LSTM—when they are applied to varied datasets of stock symbols over multiple years, highlighting their ability to incrementally gather and preserve knowledge. Through detailed testing and evaluation, this paper critically assesses the efficacy of various machine learning approaches within these specific contexts.

Proposed Methodology

In line with the available theoretical and practical research, our approach compares the performance of different regression models (e.g., decision trees, ridge regression, random forests, etc.) in predicting stock prices. Analyze the strengths and weaknesses of each model in terms of prediction accuracy, computational efficiency, and robustness to different market conditions. We have also compared the models with different symbols and for different years of data.

Additionally, this study assesses the effectiveness of incremental learning techniques in updating regression models with the arrival of new data. We explore methods for integrating new information into the model while maintaining previously acquired knowledge and adapting to evolving market conditions. Furthermore, this research investigates the application of ensemble learning techniques, such as stacking and boosting, to amalgamate predictions from various regression models, thereby enhancing accuracy and stability. The effectiveness of ensemble approaches in compensating for the limitations of individual models and delivering more reliable predictions is examined.

This investigation delves into the application of transfer learning techniques to predict stock prices across diverse markets or asset classes, focusing on the capability of models that have been pre trained in one market to be effectively fine-tuned or adapted for use in another, especially in situations where historical data is limited.

Data collection

Data has been gathered from Yahoo Finance using Python. The Python library finance facilitates the downloading of financial data from Yahoo Finance. This tool offers an easy and efficient method for accessing extensive financial data associated with a specific stock symbol, such as historical price data, financial statements, and additional details [38].

Implementation Methodology

In this study, we've employed a technique known as continual learning to enhance the accuracy and adaptability of our stock price prediction models. Continual learning, in simple terms, refers to the process of updating and refining our models over time as new data becomes available. This approach allows our models to learn from past experiences while also incorporating fresh information to improve their predictive capabilities.

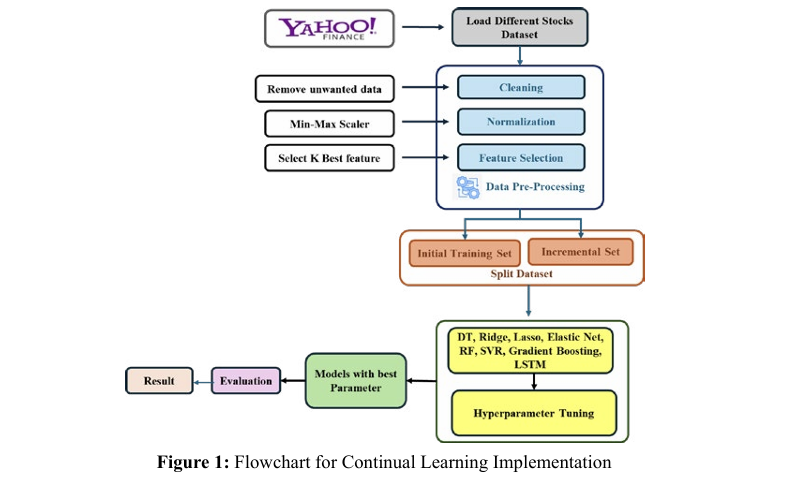
Figure 1 in the paper illustrates an in-depth flowchart of our methodology designed for continual learning. Initially, we load stock data from Yahoo Finance, which is the first step in our process. Following data acquisition, the dataset undergoes preprocessing which includes cleaning, normalizing using the MinMax scaler, and feature selection. Post-preprocessing, the dataset is split into two segments: an initial training set and an incremental set. The initial training set serves to initially train our regression models, giving them a basic grasp of stock price trends. After this initial training, the models are periodically updated with the incremental set, which includes newer data that was not available in the initial phase.

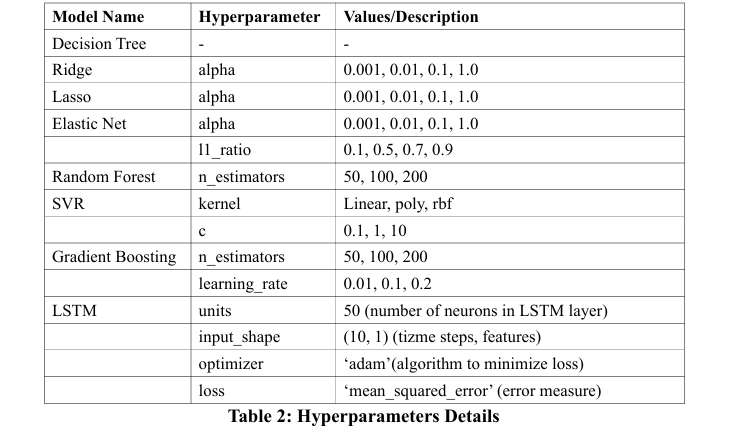
This method of continuously integrating new data ensures our models stay current and attuned to shifts in market dynamics. Subsequently, after splitting the data, we conduct hyperparameter tuning using GridSearchCV for all models, identify the optimal parameters, and enhance model training with these parameters. Detailed in Table 2 are the specific hyperparameters employed for various models. Finally, we perform performance analysis and model evaluation using metrics such as mean squared error and R-squared error to obtain the ultimate results.

This process of continual learning allows our models to adapt and improve over time, which enhances their ability to make precise stock price forecasts. Through this repeated, adaptive approach, we strive to develop strong and dependable predictive models capable of effectively managing the complexities of the stock market environment.

Results and Discussions

This segment evaluates the performance of different machine learning models used to forecast stock prices for three significant stocks: TCS.NS, INFY.NS, and RELIANCE.NS. The effectiveness of these models was gauged using their mean squared error (MSE) and R-squared (R²) metrics across four forecasting periods: 5, 10, 15, and 20 years.

Model Performance Overview

Overall, the ensemble techniques, specifically Random Forest and Gradient Boosting, outperformed others in most evaluations and across various prediction intervals. The LSTM model also displayed encouraging outcomes, especially in its early predictions.

* Detailed Result by Model

â? Decision Tree : The Decision Tree model consistently recorded a mean squared error (MSE) of 0.0 and an R-squared (R²) value of 1.0 for all prediction periods and stocks, demonstrating an ideal fit to the training dataset. However, this perfect score may indicate overfitting, potentially reducing its effectiveness on new, unseen data.

â? Random Forest: Random Forest demonstrated strong performance with low mean squared errors (MSEs) and high R-squared (R²) values for all stocks and across all prediction intervals. For example, for TCS.NS with a 10-years forecast, the initial MSE was 177.31 and the R² was 0.9997, highlighting its effectiveness in accurately capturing fluctuations in stock prices.

â? Gradient Boosting: Likewise, Gradient Boosting recorded low mean squared errors (MSE) and high R-squared (R²) scores, confirming its effectiveness in progressively enhancing its accuracy during the training phase. Its capability was especially evident in the case of RELIANCE.NS over a 15-years forecasting period, where it achieved an incremental MSE of 539.91 and an R² of 0.9907.

â? LSTM: The LSTM model initially displayed excellent results, achieving almost zero mean squared errors (MSEs) and very high initial R-squared (R²) values. However, its performance over time showed fluctuations, suggesting possible overfitting problems that require additional analysis

â? Ridge, Lasso, and Elastic Net: Compared to the ensemble methods, these models exhibited average mean squared error (MSE) and R-squared (R²) values. For instance, the incremental MSE for the Ridge model on INFY.NS over a 20-years period was 497.60, with an R² of 0.9931.

â? SVR: SVR showed higher mean squared errors (MSEs) and lower R-squared (R²) values, indicating it was less effective for these datasets. Specifically, its performance on RELIANCE.NS over a 10-day period resulted in an incremental MSE of 1639.18 and an R² of 0.9673.

Summary Table

Table 3 provides a detailed analysis of various machine learning models applied to predict TCS.NS stock data over periods ranging from 5 to 20 years. The models evaluated include Decision Trees, Ridge, Lasso, Elastic Net, Random Forest, Support Vector Regression (SVR), Gradient Boosting, and LSTM networks, with performance metrics reported in terms of Mean Squared Error (MSE) and R-squared (R2) values initially and after incremental updates.

Decision Trees maintained optimal performance (MSE=0.0, R2=1.0) across all periods, showing no deterioration in predictive accuracy. Conversely, Ridge, Lasso, and Elastic Net demonstrated initial efficacy but experienced some decline in R2 with longer timeframes. Random Forest and Gradient Boosting showed notable resilience, with minimal performance reductions and consistently high R2 values post-update. SVR, however, underwent significant performance losses, particularly in MSE, upon updates. The LSTM started with minimal MSE but saw a significant R2 drop in longer term predictions, indicating potential challenges in sustaining accuracy over prolonged periods.

This evaluation underscores the varied durability and adaptability of these models to incremental data updates, providing crucial considerations for model selection based on long-term predictive reliability in practical settings.

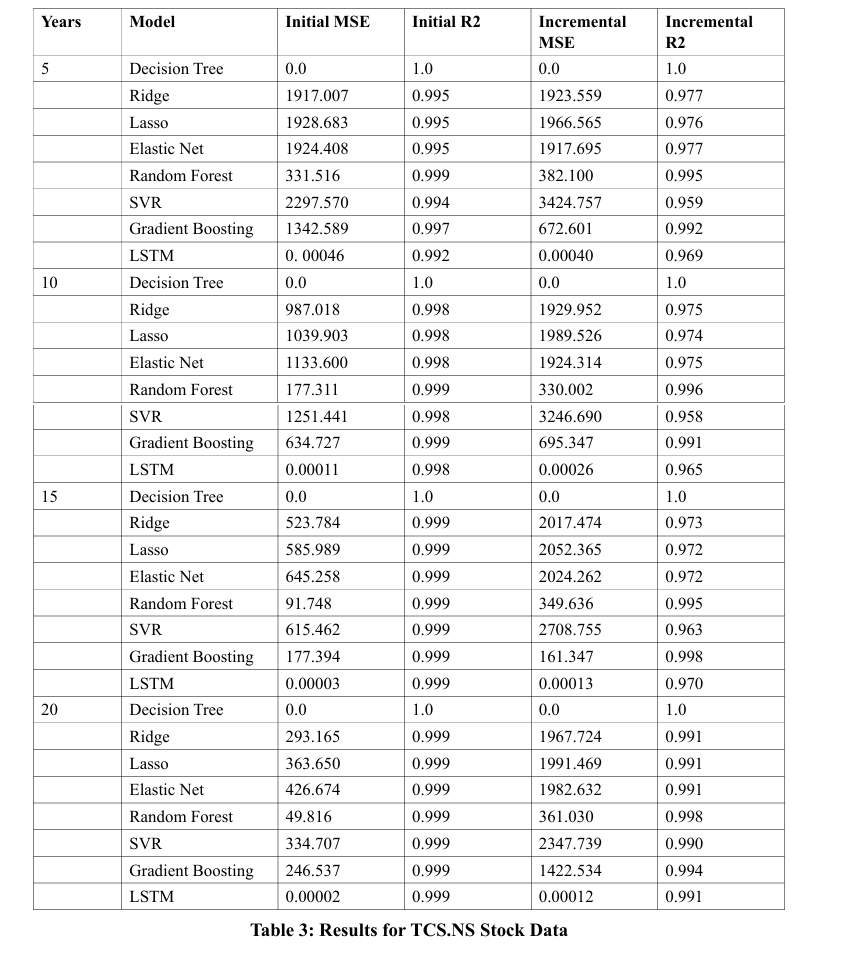
Table 4 offers a detailed analysis of the efficacy of various machine learning models in forecasting Infosys stock data across different time spans (5, 10, 15, and 20 years). The models assessed include Decision Trees, Ridge, Lasso, Elastic Net, Random Forest, Support Vector Regression (SVR), Gradient Boosting, and LSTM networks. The evaluation metrics used are Mean Squared Error (MSE) and R-squared (R2), assessed both initially and after periodic updates.

The Decision Tree consistently delivers optimal performance, with an MSE of 0.0 and an R2 of 1.0 in all tested periods, showcasing unparalleled accuracy. Other models like Ridge, Lasso, and Elastic Net initially perform well but exhibit a noticeable increase in MSE and a decline in R2 with updates, indicating a decrease in predictive reliability over time. Conversely, the Random Forest and Gradient Boosting models demonstrate high resilience, maintaining robust performance metrics, particularly Gradient Boosting which shows enhanced R2 in the 10-year evaluations. However, SVR and LSTM experience significant deteriorations in both MSE and R2 after updates, suggesting a relative instability for long-term predictions. This comparative study emphasizes the critical need for selecting machine learning models based on their sustained accuracy and stability over prolonged durations, especially in dynamic financial environments.

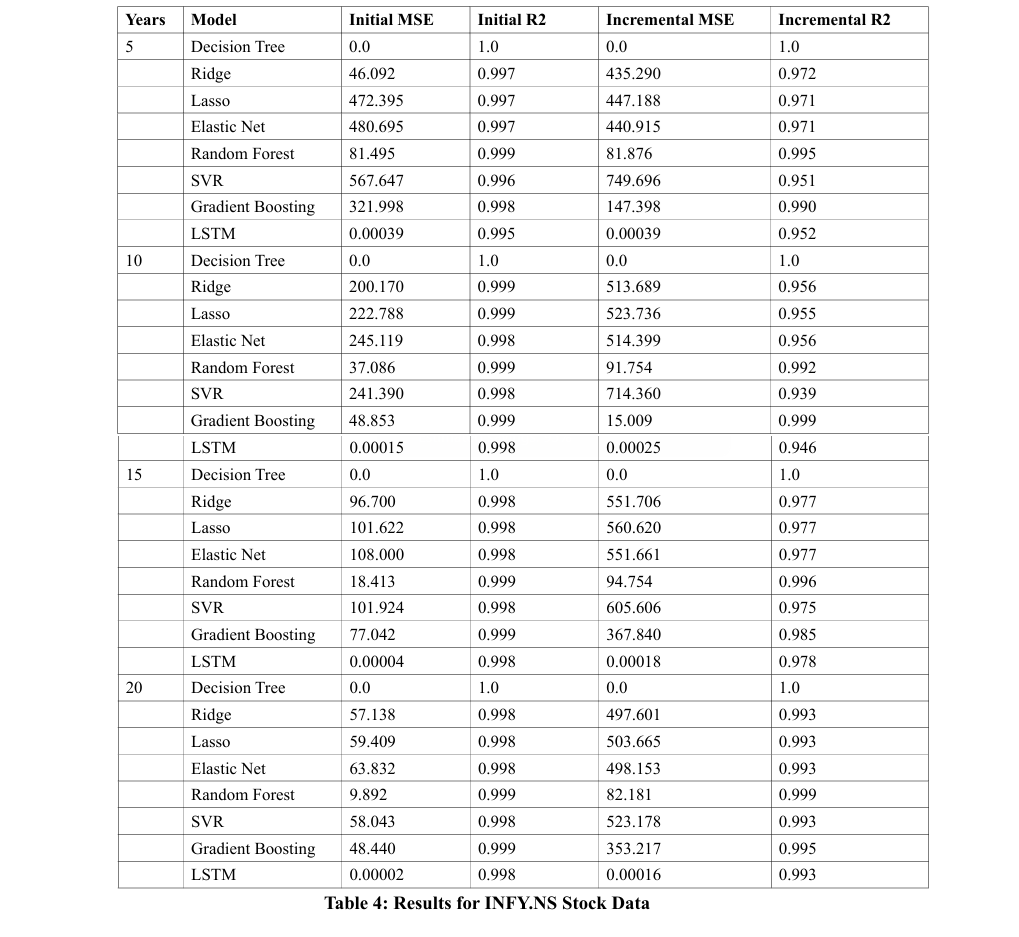
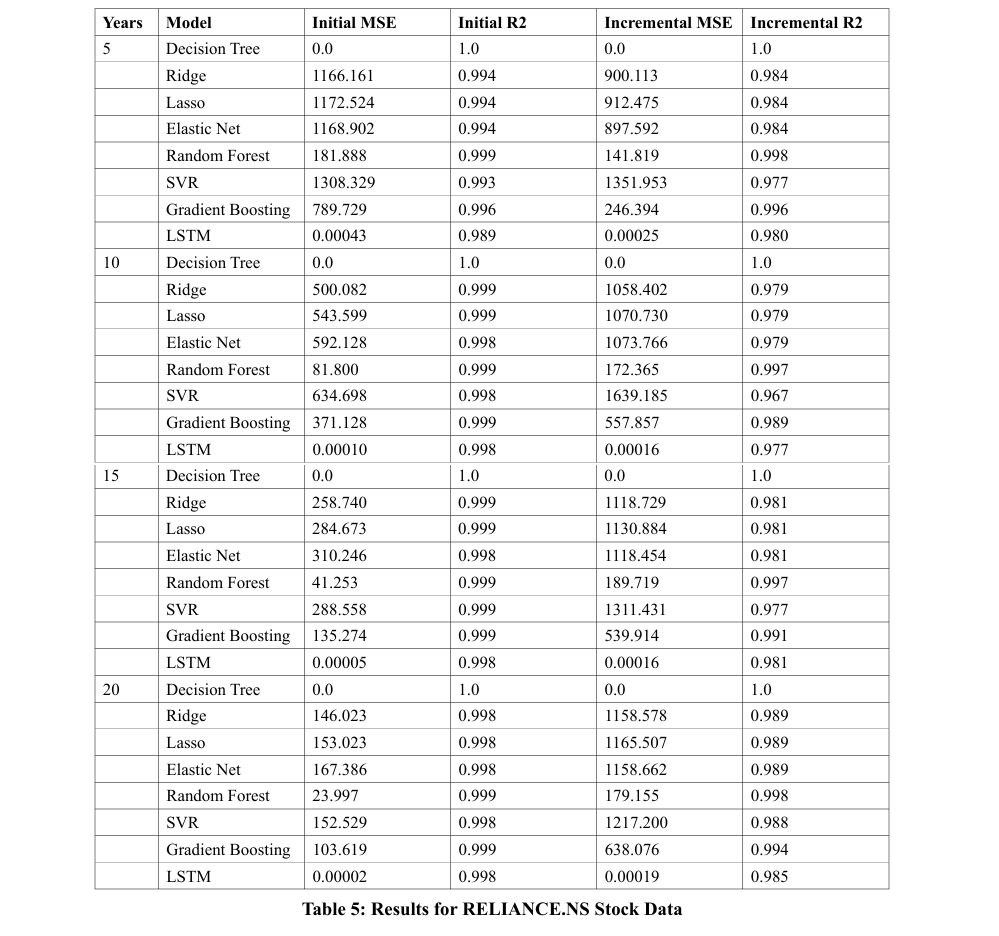
Table 5 provides an evaluative comparison of various machine learning models used for predicting Reliance stock data over different forecasting periods (5, 10, 15, and 20 years), using Mean Squared Error (MSE) and R-squared (R2) as evaluative metrics before and after incremental updates.

The Decision Tree model demonstrates exemplary consistency, achieving an MSE of 0.0 and an R2 of 1.0 throughout, reflecting its unwavering accuracy. Linear models like Ridge, Lasso, and Elastic Net show robust initial metrics which slightly diminish over time, indicating a susceptibility to long-term data shifts. In contrast, the Random Forest model maintains near-perfect resilience, with slight fluctuations but generally high R2 values. The SVR and LSTM models, however, face more significant performance shifts, with notable MSE increases for SVR and R2 decreases for LSTM, suggesting challenges in long-term stability. Meanwhile, Gradient Boosting proves efficient, with minor MSE increases and stable R2, illustrating good long-term performance retention.

This review underscores the varied durability of machine learning models in long-term financial forecasting, emphasizing the necessity for model selection that considers both stability and adaptability over extended periods. Decision Trees and Random Forest emerge as particularly robust options, whereas SVR and LSTM might necessitate more regular updates to remain effective.

Graphs and Charts

Figure 2 presents a comparative analysis of predictive modeling for the TCS.NS metric, employing data spanning various timeframes. Each set of models is appraised based on Mean Squared Error (MSE) and the coefficient of determination (R2).

� Over a 5-year span, both the Random Forest and Gradient Boosting algorithms exhibit elevated initial and subsequent MSE readings, coupled with R2 scores approaching unity. This trend may suggest a propensity for these models to resonate exceedingly well with the training dataset, potentially at the expense of their predictive applicability to new data sets, hinting at possible overfitting.

â? Evaluating a 10-year interval, the same models, Random Forest and Gradient Boosting, persist in demonstrating heightened MSEs. Despite this, the initial and subsequent R2 metrics are maintained at lofty levels across all models, signaling robust variance explanation by the models.

� Advancing to a 15-year timeline, there is a perceivable decrement in the MSE values for the Random Forest and Gradient Boosting frameworks when contrasted with the shorter-term datasets, insinuating an enhancement in model performance with the extension of the duration. The consistency of high R2 values across the models remains unaltered, indicating stable predictive strength.

� In the assessment of a 20-year period, a general reduction in MSE values suggests an overall amelioration in model accuracy. Remarkably, the R2 values are exceptionally high, with the LSTM model standing out, which reflects a superior capability of the models to capture and elucidate the variance within the extensive duration dataset.

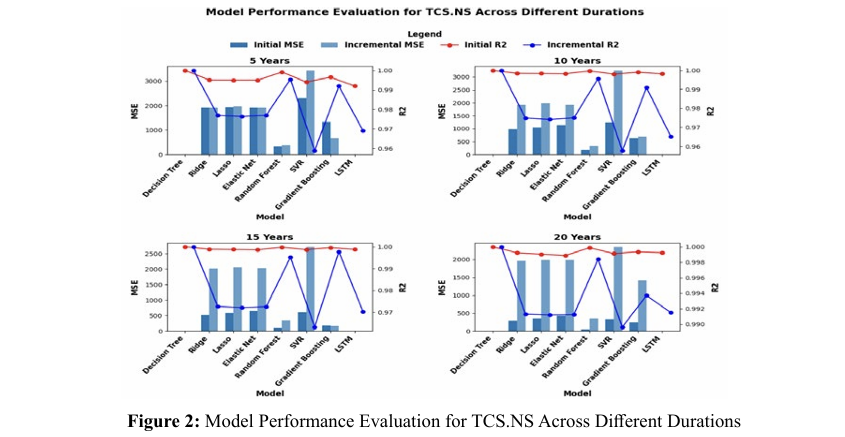
Figure 3 delineates a longitudinal comparison of various computational models analyzing INFY.NS metrics over incrementally expanding timelines.

� For the quinquennial scope, the Mean Squared Error (MSE) showcases a diverse range of outcomes across the evaluated models, with the SVM model particularly reporting elevated MSE f igures. Despite this variability, the coefficient of determination (R2) remains consistently elevated across the board, indicating a robust capacity of the models to account for the variability of the dependent variable.

â? Progressing to the decennial benchmark, a similar variability in MSE is observed among the different models. Notably, there is a marginal regression in the R2 values for some models when juxtaposed with the 5-year data set, yet the values still reflect a substantial explanatory power of the models.

� Extending the evaluation to 15 years, an upsurge in the MSE for certain models, such as the SVM, is notable. Conversely, the R2 values for most models are remarkably high and proximal to unity, signifying an impressive congruence between the predicted and observed values.

� Upon scrutinizing a 20-year interval, a general downtrend in MSE is evident among the majority of models, implying an enhancement in predictive precision over time. Concurrently, the R2 values sustain their ascendancy, with the LSTM model, in particular, demonstrating exemplary predictive alignment.

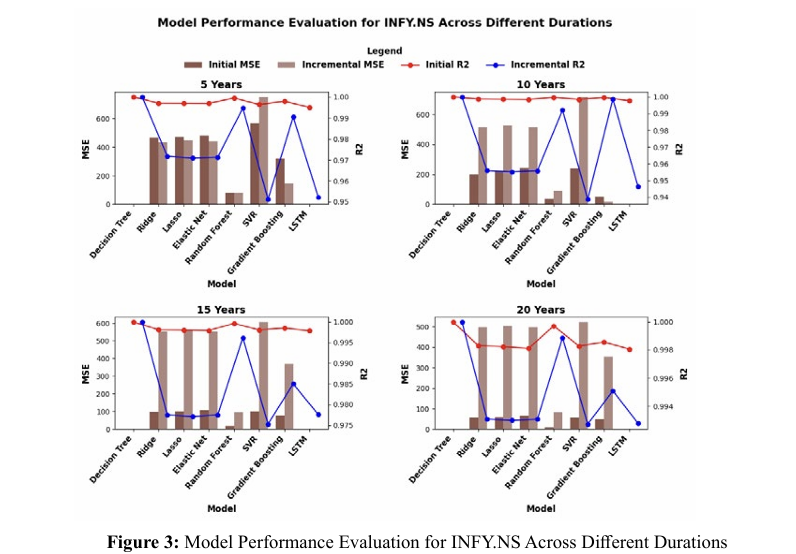
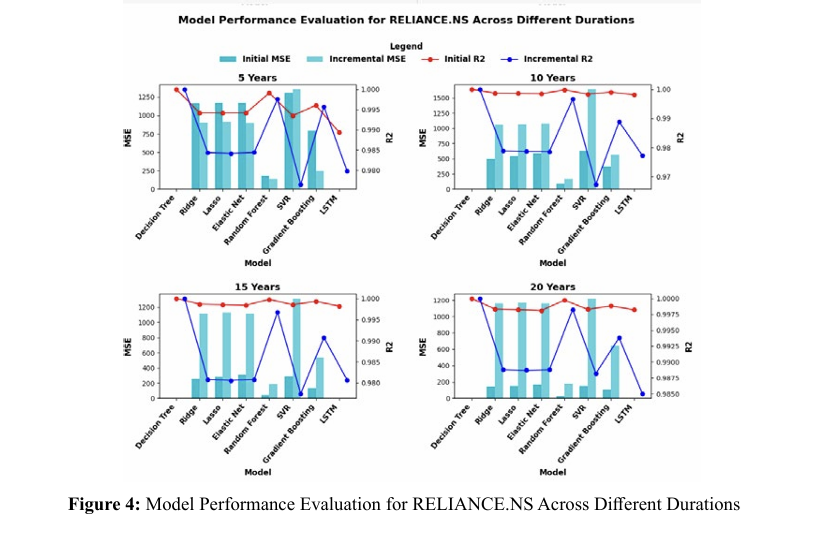
Figure 4 provides an analytical review of model efficacy over differing temporal scales for the RELIANCE.NS metric.

� Within the initial five-year spectrum, the depicted bar heights and R2 trajectories reveal disparities in model efficacy, with certain models registering elevated MSEs while maintaining R2 values in proximity to the ideal score of 1.

� A decade-long evaluation maintains the general trends observed in the five-year assessment, albeit with some discernible shifts in R2 indices amongst the various models.

â? Expanding the scope to fifteen years, there is a noticeable diversification in MSE results among the models, yet the R2 scores predominantly sustain their high values, underscoring the models’ consistent explanatory power.

â? The twenty-year horizon illustrates a downward shift in MSE readings across the board, indicating an augmentation in model precision with the passage of time. The R2 values are markedly high, reinforcing the models' adeptness in capturing the dataset’s variability.

In an analysis of performance metrics across datasets covering intervals of 5, 10, 15, and 20 years for the symbols TCS.NS, INFY.NS, and RELIANCE.NS, it is evident that a 20-year dataset provides the most favorable conditions for ongoing learning. This inference is supported by a noticeable decrease in Mean Squared Error (MSE) and consistently high R-squared (R2) values across all datasets. These indicators suggest that the models not only enhanced their predictive accuracy but also retained their effectiveness in accounting for the variance in the data over a prolonged period. The ability of the models to adjust and improve with the introduction of more comprehensive data supports the conclusion that extended datasets facilitate more effective and progressive learning.

Conclusion

In this research, we evaluated eight distinct machine learning models for their accuracy in forecasting the prices of three prominent Indian stocks: TCS.NS, INFY.NS, and RELIANCE.NS over different time frames. The findings reveal that Random Forest and Gradient Boosting models outperformed others consistently across all stocks and periods, achieving low mean squared errors and high R-squared values. These models demonstrated strong capability in managing the intricacies of stock market data, indicating their potential effectiveness in applications related to f inancial forecasting.

The Decision Tree model consistently performs perfectly across all time periods, maintaining zero error and an R² of 1.0. In contrast, Ridge, Lasso, and Elastic Net models exhibit increasing Mean Squared Error (MSE) and decreasing R² values over time, indicating a decline in performance. For example, Ridge's MSE increases range from 72.41% to 1918.29%, with R² reductions of up to 2.30% to 5.29% over 20 years. Lasso and Elastic Net follow similar patterns, with MSE rises between 137.12% and 1879.35%, and R² drops of 4.42% to 5.47%. The Random Forest model shows a moderate decline, with MSE increases up to 625.13% and R² reductions up to 0.40%. SVR experiences significant performance drops, with MSE increases of 49.07% to 601.35% and R² decreases up to 4.01%. Gradient Boosting yields mixed results, with MSE increases up to 516.90% and R² reductions up to 0.50%. LSTM demonstrates variability, showing short-term improvements but longer-term declines, with MSE increases up to 500.00% and R² drops up to 4.31%. Overall, while Decision Tree remains consistently reliable, Ridge, Lasso, Elastic Net, and SVR show substantial performance deterioration. Random Forest and Gradient Boosting are relatively more stable, and LSTM has potential for short-term improvement but declines over longer periods.

Future research should focus on incorporating feature engineering and refined hyperparameter optimization to improve the predictive capabilities of models like SVR, Ridge, Lasso, and Elastic Net. Furthermore, investigating hybrid models that merge the advantages of ensemble methods with neural networks could provide valuable insights. Employing cross-validation and external validation strategies will be essential to ensure the robustness and dependability of these predictive models.

Acknowledgments

The authors would like to acknowledge C. K. Pithawala College of Engineering and Technology, MG research organization and Elite Technocrats for financial support as well as provide a facility for entire research work.

References

1. Mendez, J. A., & Eaton, E. (2022). How to reuse and compose knowledge for a lifetime of tasks: A survey on continual learning and functional composition. arXiv preprint arXiv:2207.07730.

2. Wang, Z., Liu, L., Duan, Y., & Tao, D. (2022, June). Continual learning through retrieval and imagination. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 36, No. 8, pp. 8594-8602).

3. Maxwell, D., Meyer, S., & Bolch, C. (2021). DataStory™: an interactive sequential art approach for data science and artificial intelligence learning experiences. Innovation and Education, 3(1), 1-13.

4. Mousavi, H., Buhl, M., Guiraud, E., Drefs, J., & Lücke, J. (2021). Inference and learning in a latent variable model for Beta distributed interval data. Entropy, 23(5), 552.

5. Abed-Alguni, B. H., Alawad, N. A., Al-Betar, M. A., & Paul, D. (2023). Opposition-based sine cosine optimizer utilizing refraction learning and variable neighborhood search for feature selection. Applied Intelligence, 53(11), 13224-13260.

6. Hu, Z., Xing, Y., Gu, W., Cao, D., & Lv, C. (2022). Driver anomaly quantification for intelligent vehicles: A contrastive learning approach with representation clustering. IEEE Transactions on Intelligent Vehicles, 8(1), 37-47.

7. Zhang, C., Liu, J., Zhi, J., Zhang, X., Wang, J., & Wu, Z. (2023, August). OceanCL-IDS: A Continual Learning based Intrusion Detection System for Ocean-going Ship Satellite Communication Network. In 2023 7th International Conference on Transportation Information and Safety (ICTIS) (pp. 1150-1155). IEEE.

8. Rane, N., Choudhary, S., & Rane, J. (2023). Blockchain and Artificial Intelligence (AI) integration for revolutionizing security and transparency in finance. Available at SSRN 4644253.

9. Pinilla, S., Mishra, K. V., Shevkunov, I., Soltanalian, M., Katkovnik, V., & Egiazarian, K. (2023). Unfolding-aided bootstrapped phase retrieval in optical imaging: Explainable AI reveals new imaging frontiers. IEEE Signal Processing Magazine, 40(2), 46-60.

10. Cossu, A., Ziosi, M., & Lomonaco, V. (2021, December). Sustainable artificial intelligence through continual learning. In CAIP 2021: Proceedings of the 1st International Conference on AI for People: Towards Sustainable AI, CAIP 2021, 20-24 November 2021, Bologna, Italy (p. 103). European Alliance for Innovation.

11. Parisi, G. I., & Kanan, C. (2019). Rethinking continual learning for autonomous agents and robots. arXiv preprint arXiv:1907.01929.

12. Vallabha, G. K., & Markowitz, J. (2022, June). Lifelong learning for robust AI systems. In Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications IV (Vol. 12113, p. 1211304). SPIE.

13. Hassanpour, A., Moradikia, M., Yang, B., Abdelhadi, A., Busch, C., & Fierrez, J. (2022). Differential privacy preservation in robust continual learning. IEEE Access, 10, 24273-24287.

14. Tang, D., Huang, Y., Che, Y., Yang, C., Pu, B., Liu, S., & Li, H. (2024). Identification of platelet-related subtypes and diagnostic markers in pediatric Crohn’s disease based on WGCNA and machine learning. Frontiers in Immunology, 15, 1323418.

15. Kovoor, J. G., Bacchi, S., Gupta, A. K., O'Callaghan, P. G., Abou�Hamden, A., & Maddern, G. J. (2023). Artificial intelligence clinical trials and critical appraisal: a necessity. ANZ journal of surgery, 93(5).

16. Wang, X., & Atluri, S. N. (2017). Computational methods for nonlinear dynamical systems. Mechanical Engineering Reviews, 4(2), 17-00040.

17. Tarp, S. (2014). Theory-Based Lexicographical Methods in a Functional Perspective. An Overview [Theoriebasierte lexikographische Methoden aus funktionaler Perspektive. Ein Überblick/Méthodes en lexicographie théorique du point de vue fonctionnel. Une vue d’ensemble]. Lexicographica, 30(2014), 58-76.

18. Safonov, I. M., Shulika, A. V., Sukhoivanov, I. A., & Lysak, V. V. (2004, December). Model for self-consistent analysis of arbitrary MQW structures. In Physics and Applications of Optoelectronic Devices (Vol. 5594, pp. 33-44). SPIE.

19. Safonov, I. M., Shulika, A. V., Sukhoivanov, I. A., & Lysak, V. V. (2004, December). Model for self-consistent analysis of arbitrary MQW structures. In Physics and Applications of Optoelectronic Devices (Vol. 5594, pp. 33-44). SPIE.

20. Hosseini, S., Pourmirzaee, R., Armaghani, D. J., & Sabri, M. M. (2023). Prediction of ground vibration due to mine blasting in a surface lead–zinc mine using machine learning ensemble techniques. Scientific Reports, 13(1), 6591.

21. Zhang, H., Saravanan, K. M., & Zhang, J. Z. (2023). Deepbindgcn: Integrating molecular vector representation with graph convolutional neural networks for protein–ligand interaction prediction. Molecules, 28(12), 4691.

22. Abba, S. I., Linh, N. T. T., Abdullahi, J., Ali, S. I. A., Pham, Q. B., Abdulkadir, R. A., ... & Anh, D. T. (2020). Hybrid machine learning ensemble techniques for modeling dissolved oxygen concentration. IEEE Access, 8, 157218-157237.

23. Alnaqbi, A. J., Zeiada, W., Al-Khateeb, G. G., Hamad, K., & Barakat, S. (2023). Creating rutting prediction models through machine learning techniques utilizing the long-term pavement performance database. Sustainability, 15(18), 13653.

24. Wang, L., Zhang, X., Su, H., & Zhu, J. (2024). A comprehensive survey of continual learning: theory, method and application. IEEE Transactions on Pattern Analysis and Machine Intelligence.

25. Kim, G., Xiao, C., Konishi, T., Ke, Z., & Liu, B. (2022). A theoretical study on solving continual learning. Advances in neural information processing systems, 35, 5065-5079.

26. Kim, J. S., Kim, S. H., & Lee, K. H. (2023). Diversified adaptive stock selection using continual graph learning and ensemble approach. IEEE Access. 27. Zhou, D. W., Sun, H. L., Ning, J., Ye, H. J., & Zhan, D. C. (2024). Continual learning with pre-trained models: A survey. arXiv preprint arXiv:2401.16386.

28. Awasthi, A., & Sarawagi, S. (2019, January). Continual  learning with neural networks: A review. In Proceedings of the ACM India Joint International Conference on Data Science and Management of Data (pp. 362-365).

29. Parisi, G. I., Kemker, R., Part, J. L., Kanan, C., & Wermter, S. (2019). Continual lifelong learning with neural networks: A review. Neural networks, 113, 54-71.

30. Khan, V., Cygert, S., Twardowski, B., & TrzciÅ?ski, T. (2023). Looking through the past: better knowledge retention for generative replay in continual learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision (pp. 3496-3500).

31. Liu, S., Wang, B., Li, H., Chen, C., & Wang, Z. (2023). Continual portfolio selection in dynamic environments via incremental reinforcement learning. International Journal of Machine Learning and Cybernetics, 14(1), 269-279.

32. de Carvalho, M., Pratama, M., Zhang, J., Haoyan, C., & Yapp, E. (2024). Towards Cross-Domain Continual Learning. arXiv preprint arXiv:2402.12490.

33. Yilmaz, F. M., & Yildiztepe, E. (2024). Statistical evaluation of deep learning models for stock return forecasting. Computational Economics, 63(1), 221-244.

34. Semola, R., Hurtado, J., Lomonaco, V., & Bacciu, D. (2024). Adaptive Hyperparameter Optimization for Continual Learning Scenarios. arXiv preprint arXiv:2403.07015.

35. Pan, Z., Jiang, Y., Song, D., Garg, S., Rasul, K., Schneider, A., & Nevmyvaka, Y. (2024). Structural Knowledge Informed Continual Multivariate Time Series Forecasting. arXiv preprint arXiv:2402.12722.

36. Huang, S., Liu, Z., Deng, Y., & Li, Q. (2024). Incremental Learning of Stock Trends via Meta-Learning with Dynamic Adaptation. arXiv preprint arXiv:2401.03865.

37. Junge, K. (2023, November 1). yfinance: 10 Ways to Get Stock Data with Python - Kasper Junge - Medium. Medium. https://medium.com/@kasperjuunge/yfinance-10-ways-to get-stock-data-with-python-6677f49e8282