AI Uncertainty Based on Rademacher Complexity and Shannon Entropy

Introduction

Artificial Intelligence (AI) based on deep learning neuron networks are widely used in CT imaging, pattern recognitions, medical diagnosis, and scientific computing. Usually large neuronal network architectures are first selected for a specific purpose and the neuron network are trained by large samples of the data from the specific applications such as CT imaging for medical diagnosis. Secondly fully trained neuron networks are used as AI model to diagnose unknown patterns for example CT images to be normal or abnormal ones. Current AI model depends upon the large samples training methods and control the error rate as small as possible.

However, in practice one wishes to control the error rate to be approaching zero or even to be zero in many lives related applications such as in medical diagnosis. It is therefore an important task for AI designers to design an AI model that can control the error rate in an efficient way so that AI model can be used in life related crucial applications. There are huge references in analyzing upper and lower bounds for neuron network errors in accurately recognizing the patterns. However very few papers addressed AI design methods to control the error rates to be zero or approaching zero as much as desired in applications. In this article, we are investigating in this direction by providing both a theory and a pragmatic methodology.

Background

As Artificial Intelligence (AI) is based on trained various neuron networks such as CNN or RNN and becomes wide-spreading and applied in various industries, AI uncertainty investigations based on various neuron networks obviously becomes more and more important in practical applications in that probability errors from data driven AI model itself and errors from nuisance or noise in engineering applications are inevitable in practice. Given a problem with certain complexity measured by different measures such as Rademacher complexity and Vapnik-Cheronenkis (VC) dimensions etc., it is desired in practice that one can design a neuron network trained by deep learning algorithms so that the trained neuron network can accurately classify patterns with no errors or even small errors. It is therefore our wish that after deep learning training, neuron network can classify the test patterns with no errors or with errors approaching zero. Errors of two-layer forward neuron networks for classification problems and approaching functions were theoretically and in quantity investigated in [1, 2].

Upper and lower bounds depending upon various parameters of neuron networks are derived. In this paper, however, by applying Shannon’s mathematical theory on communications channel coding [3]. We address the pattern classification errors of trained neuron networks from Shannon’s entropy perspective. We provide a generalized framework to discuss AI uncertainty, capacity and evolution with the existence of probability errors from data driven AI models and errors from nuisance and noise in AI applications [1- 3]. We prove that a sufficient and necessary condition that ensures classification error of trained neuron network can approach zero as much as desired. Other sufficient conditions are derived as well. We do not limit our neuron network structures into specific CNN or RNN or two-layer forward neuron networks, but provide a more generalized discussion on the errors introduced at trained neuron network phase and at application phase with nuisance and noise. Learning algorithms are therefore not included in this letter paper.

In Section III , a methodology is described on how to design an AI system that can ensure an AI evolution and reduce mistakes in AI systems . Section IV is devoted to theory and analysis of zero error approaching AI system by relating Rademacher complexity to Shannon’s transmission rate in communication theory. We derive several sufficient and necessary conditions for AI zero error approaching classification problem. An analysis is done in this section and sufficient /necessary conditions are derived for zero error approaching AI system. An examples of simple “coding” method is given for zero error approaching AI system in Section V. This paper is concluded with Section VI in which major results are summarized.

Methodology

Considering a scenario in which a clinic is doing CT scanning and then needs an AI to process and identify COVID-19 lung images from normal ones per second. We wish to design an AI to classify the normal images and COVID-19 images with error approaching zero or being zero during a given interval time. We first summarize our methodology as in the following steps and then explain our AI design methodology.

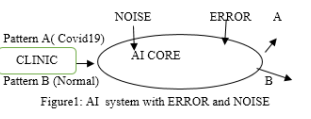
The principle is to apply Shannon’s channel coding theory thought to ensure zero error approaching property of designed AI system. As illustrated in Figure 1,

1. AI core is designed with a proper neuron network architecture such as CNN, RNN or forward 2-layer neuron network with each neuron with sigmoid functions property. ERROR in figure1 denotes the system error due to training. NOISE denotes the nuisance in real applications.
2. A training is completed with Back Propagation(BP) algorithms with large known samples such as CT imaging samples for COVID19 lung images and normal lung images. There we have 2 types of patterns, one is COVID19 lung CT images and the other pattern is normal lung images without COVID19 virus affections. Note that there is an error rate (denoted by ERROR in figure 1) in this AI core in that normal lung images may be wrongly classified into COVID19 case.
3. Given ERROR obtained at 2), if ERROR satisfies conditions which are to be discussed in the following section, a simple or advanced coding method exists so that the images can be classified with error approaching zero.
4. For identified failure images, go to 2) and train the failed samples so that AI evolves to a higher level.
5. The process is completed until there are no more failed images. This process can be thought as an adaptive and evolving AI methodology.

Theory and Analysis

In this section, we first relate neuron network based AI system to a communication channel and then derive two theorems regarding zero error approaching property by relating Rademacher complexity to Shannon’s transmission rate and Shannon’s entropy. We first overview the main results of Shannon’s communication theory by reviewing Shannon’s definition on channel/AI capacity and information transmission rate. Then we present two theorems about zero error approaching of an AI model for pattern classification problems. We will show that an AI system and a communication channel resemble in principle. First the following Shannon condition are well known to ensure a proper encoding for zero error approaching communication channels.

Rs < C

C = Max (H(x)-  H_y(x))                   (1)

where C between 0 and 1 is defined as the channel/AI capacity in Shannon theory for a noisy channel, and Rs is Shannon transmission rate between 0 and 1. Max denotes maximum value and H(x) denotes Shannon information x’s entropy and H_y(x) denotes Shannon conditional entropy [3]. Condition (1) by Shannon theory indicates that the transmission rate Rs must not exceed channel/AI capacity C in order to recover the original information exactly by a proper encoding method with errors approaching or being zero [3].

Now with an AI model for classification problems, it is natural to relate AI system to a communication channel with the following confronted problem: given a pattern classification problem with known complexity measured by a known Rademacher complexity, to what extend a neuron network AI should be trained so that AI deep learning neural network with a certain known recognition error rate has the ability to recognize all patterns/symbols correctly in a “coding” way with classification errors approaching to zero or being zeros? In AI system, Hy(x) can be interpreted as the total errors introduced by the trained AI model and the errors introduced by inevitable nuisance and physical noises in real AI applications, see Figure 1 [1, 2]. We wish to explore the conditions under which an AI system can tolerant such total errors and in a way can reach  a zero error approaching or a zero error recognition rate. In the following, we will show that based on definition of traditional Rademacher complexity and Shannon coding theory, sufficient/ necessary conditions can be derived for zero error AI system or zero error approaching AI system.

It is well known that classical Rademacher complexity is defined as in the following equation (2).

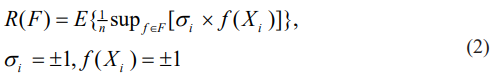
Where E denotes ensemble, F denotes the problem’s hypothesis space. R(F) lies between value of 0 and 1 with value of 1 denoting the maximum complexity and value of 0 minimum complexity. For a given problem of transmitting a symbols series of either 1 or 0, Shannon transmission rate Rs of equation (1) in Shannon theory is closely related to classical Rademacher complexity R(F) defined in equation (2), where F denotes the hypothesis function space of given problems.

To show this, we only need to relate the definition of classical Rademacher complexity R(F) in equation (2) to Shannon communication channel conditions of equation (1). When Rademacher complexity R(F) is zero, that means a fixed constant 1 or 0(-1) is transmitted via a channel, thus Shannon rate Rs is constant 1.0. When Rademacher complexity R(F) is non-zero, that means an alternative 1 or 0(-1)’s is transmitted via a channel in a given time. Therefore, Shannon rate Rs could be equal to or even less than 1.0 because of noise error denoted by entropy Hy(x) in equation (1). Thus a Rademacher complexity R(F) for an AI system can be interpreted as related to Shannon transmission rate Rs. We denote the mapping by from Rademacher complexity R(F) to Shannon transmission rate Rs. In fact, in most cased where Rademacher complexity R(F) is non-zero, they are equivalent in the sense of communication problem. This interpretation from communication theory by taking into consideration of Rademacher complexity will help us to investigate an AI system in Figure 1.

Based on the above descriptions, we now present two conditions as follows

where ÃÃÃÃÂ???ÂÃÃÂ??ÂÃÂ?? denotes the mapping from Rademacher complexity to Shannon rate Rs. Condition A) in equation (3) indicates a condition of Rademacher complexity, and

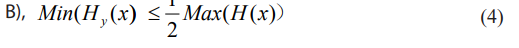
where min denotes minimum value. Condition B) in equation (4) indicates a condition regarding Shannon conditional entropy Hy(x). We now have the following theorem regarding conditions A) and B):

Theorem 1: If well-known Shannon condition in equation (1) is satisfied, either condition A) in equation (3) or condition B) in equation (4) must be valid.

The proof is a case analysis starting from equation (1). By Shannon theory on the noise channel with conditional entropy Hy(x), to ensure transmission with no errors starting from equation (1), following equation (5) must be satisfied

In practice one wishes that Hy(x) is small or close to zero in applications. Therefore, condition (9) is not valid in practice in most cases. Cases from condition (8) are valid in most cases when Hy(x)’s are small enough approaching to zero. Therefore, it is reasonable that we assume a condition of following inequality (10). We now have theorem 2 as follows.

Theorem 2: Under the condition/assumption with valid reason

Min(H_y(x) < φ{R(F)}                                 (10)

If Shannon condition of equation (1) is satisfied, condition B) of inequality (4) must be valid. If further condition is imposed

Min(Hy(x) < {R(F)} < (Max(H(x)) - Min(H (x)))        (11)

Then Shannon’s condition (1) is satisfied and inequality (4) is valid accordingly.

Proof: If Shannon condition is satisfied in (1), by theorem 1 when equation (10) is valid, inequality (4) is derived. On the other hand, under condition of inequality (11), Shannon condition (1) is obviously satisfied and inequality (4) must be valid accordingly

Theorem 2 has a significant importance in practical use. As explained before, Hy(x)’s is usually small enough approaching zero in practical AI applications. Therefore, Shannon rate Rs and Rademacher complexity R(F) are much bigger than Hy(x)’s in most cases. Without loss of generality, we can assume that Max(H(x)) =1.0 in the subsequent discussions. To show an example of theorem 2, for a moderate complexity problem R(F)<1.0,

Max(H(x)) =1.0 in the subsequent discussions. To show an example of theorem 2, for a moderate complexity problem R(F)<1.0,

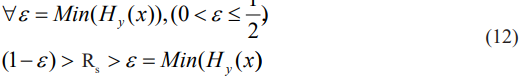
Equation (12) denotes an example that under valid assumption of equation (11), Shannon condition of inequality (1) is valid. Thus for a given moderate complexity problem, there exists an error tolerance for a channel/AI system so that a zero error approaching channel/AI system is possible by a “coding” method. Theorem 2 also indicates that for a given moderate complexity problem, AI system total errors in Figure 1, measured by entropy Hy(x)<1/2 must be controlled strictly according to theorem 2, so that a zero error approaching is possible by a proper “coding” method with Shannon rate Rs ranging in the following inequality (13).

Examples and Future Work

Suppose we are faced with classifying two patterns in Figure 1 which are COVID-19 imaging pattern denoted by A pattern and normal pattern denoted by B pattern. The rate Rs in AI system in Figure 1 is defined as the images per second rate that recognizes all A and B patterns correctly with errors approaching zero. As indicated in (12) and (13), there is a range of Rs that can be selected to ensure a zero error approaching “coding” method.

Given entropy Hy(x)<1/2 of AI model in figure 1, in our example error rate is then less than about 12% as shown in, that is, the error rate of pattern A is classified as B’s or vice versa ’s probability is less than about 12% [3]. Suppose we have A1, B1, B2, A2, A3, B3 images to be classified, a simplest “coding” method to ensure a zero error approaching is to calculate from Hy(x)<1/2 value first, and then make a decision of “coding” sequence, such as A1, B1, B2, A1, B1, B2, B2, A3, B3, A3, B3 or A1, A1, A1, B1, B2, B1, B2, B1, B2 ...etc. as long as inequality (13) is satisfied. Higher Rs value means more efficient “coding” AI system with zero error approaching property.

A more complex coding method is possible as long as inequality (13) is satisfied. Once the total errors in Figure 1 are bounded as in (13), we can design a “coding” method to ensure a zero error approaching AI system in applications. However, if condition in theorem 2 is not satisfied, zero error approaching AI system is NOT possible anyhow.

In this paper Rademacher complexity is interpreted as related to Shannon’s transmission rate in communication theory. Based on the derived results in this paper, we can possibly extend to other complexity measures such as Vapnik-Cheronenkis (VC) and Gaussian complexity by provoking the results in [6]. Criteria and condition based on other complexity measures are possible.

Conclusion

In this paper, we study AI capacity, uncertainty and evolution from communication channel coding perspective. A methodology framework based on communication channel coding insight is used and then proposed to investigate AI’s capacity and uncertainty as well as AI’s evolution. First classical Rademacher complexity is outlined and its relations with Shannon transmission rate in communication theory is interpreted. Secondly by comparing AI system to a communication channel, we are able to apply Shannon communication theory methodology to propose a zero error approaching AI “coding” method. A 1/2 criteria are derived from Shannon theory for zero error approaching condition. Several sufficient/necessary conditions are derived for zero error approaching condition for an AI. The theoretical results derived in this paper can provide an insight into zero error approaching AI framework. Methodology and example are shown on how to evolve AI to reach a lower error rate and how to utilize a simple “coding” sequence to ensure zero error approaching purpose in AI applications. The main results are summarized as follows:

1. Classical Rademacher complexity is interpreted as closely related to Shannon transmission rate in communication theory.

2. For pattern classification problems, practical sufficient and necessary conditions are derived and discussed to ensure zero error approaching property of an AI system under valid and reasonable assumptions.

Acknowledgement

The work M.Z is supported by a GXUST Fund numbered 19839. The work of T.LI is supported by Students innovation fund of GXUST numbered 202010594204.

References

1. Peter L Barlett (1998) The Sample Complexity of Pattern Classification with Neural Networks: The Size of the Weights is More Important than the Size of the Network”, IEEE Transactions on Information Theory 44: 525 – 536.
2. Andrew Barron (1993) Universal approximation bounds for superpositions of a sigmoid function, IEEE Transactions on Information Theory 39: 930-945.
3. Claude Shannon (1948) A Mathematical Theory of Communication, The Bell System Technical Journal 27: 379- 423.
4. Franco Scarselli, Ah Chung Tsoi, Markus Hagenbuchner (2018) The VC dimension of graph and recursive neural networks, Neuronal Networks 108: 248-259.
5. Zonghan Wu, Shirui Pan, Fengwen Chen, Guodong Long, Chengqi Zhang, et al. (2020) A Comprehensive Survey on Graph Neural Networks”, IEEE Transactions on Neural Network and Learning Systems XX: 1-22.
6. Davide Anguita, Alessandro Ghio, Luca Oneto, Sandro Ridella (2014) A Deep Connection Between Vapnik-Cheronenkis Entropy and Rademacher Complexity, IEEE Transactions on Neural Network and Learning Systems 25: 2202 - 2211.