Advances in Machine Learning & Artificial Intelligence(AMLAI)
ISSN: 2769-545X | DOI: 10.33140/AMLAI
Research Article - (2024) Volume 5, Issue 2
About Structure of a connected Quaternion-JUllA-Set and Symmetries of u related JULIA-Network
Received Date: Mar 12, 2024 / Accepted Date: Apr 23, 2024 / Published Date: Apr 29, 2024
Copyright: ©2024 Udo E. Steinemann. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Citation: Udo E. Steinemann. (2024). About Structure of a connected Quaternion-JUllA-Set and Symmetries of u related JULIA-Network. Adv Mach Lear Art Inte, 5(2), 01-18.
Abstract
If a variable is replace by its square and subsequently enlarged by a constant during a number of iteration-steps in quaternion-space, a network of (3) sets will be built gradually. As long as for the iteration-constant certain conditions are fulfilled, the network will consist of: an rrnbounded set (escape-set) with trajectories escaping to infinity during course of the iteration, a bounded set (prisoner-set) with trajectories tending to a sink-point and a further bounded one (JULIA-set) with a fixed-point as repeller having a repulsive effect on all points of both the other sets. The iteration will continue until the attracting sink-point of prisoner-set and the repeliing fixedpoint on JULIA-set have been found. This situation is reached if predecessor- and successor-state of the iteration became equal. The fixed-point-condition provisionally formulated in general terms of quaternions, can be separated into (3) sub-conditions. When heeding the HAMILTONian-rules for interactions of the imaginary sub-spaces of the quaternion-space, each sub-condition will be appropriate for one imaginary subspaces and independently debatable. Knowledge of fixed-points from this fundamental network will one enable to study the structure of a connected JULIA-set.
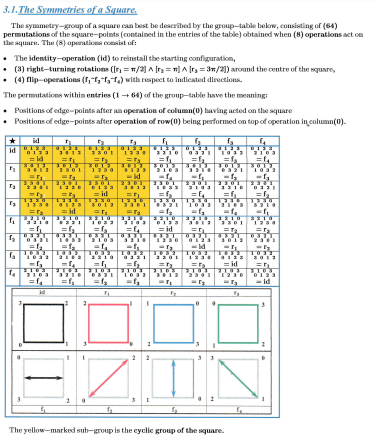
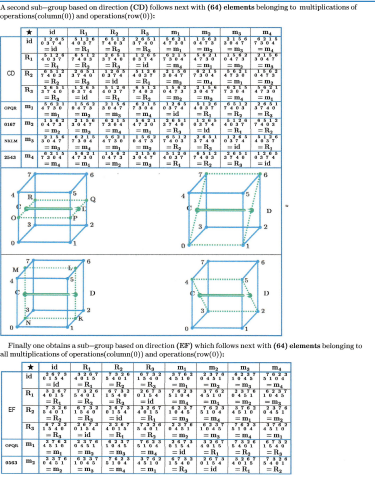
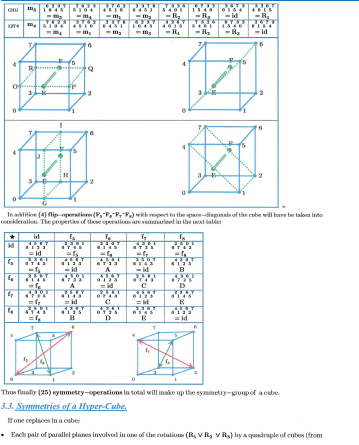
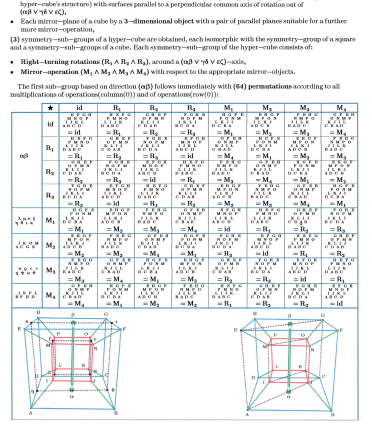
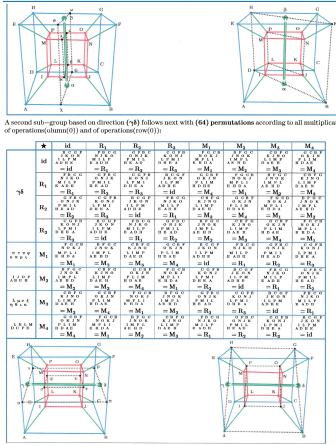
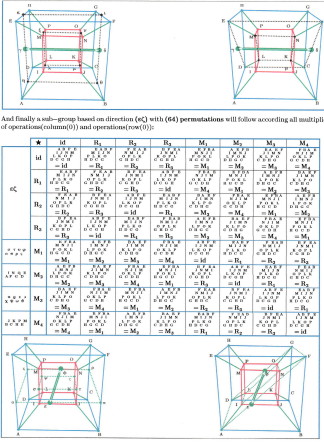
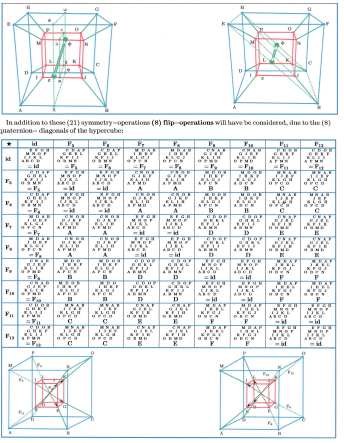
The Iteration will start from (1) on real-axis, this is not a restriction on generaiity because an appropriate scaling on real- axis can always be archived this way. It will become obvious, that the fixed-points in prisonerand JIILIA-set will depend on the iteration-constant only. Thus (16) different constants chosen appropriately will enable to arrange (16) fixed-points of JLTLIA-sets in the square-points of a hyper-cube and thereby together with the JULIA-sets to built a related JULIA-network. The symmetry-properties of this related .IULIA-network can be studied on base of a hyper-cube's symmetry-group extended by some additional considerations.
Introduction
In the following attention is appiied to the results of an iteration, which takes place in quaternion-space (a space of hyper-cubes with its space-elements) a layout of this is given next:
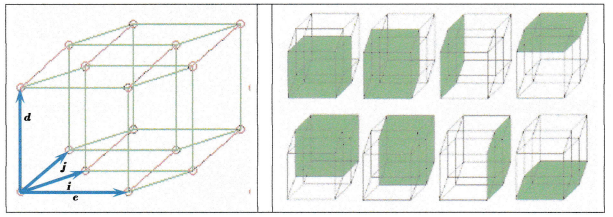
Each hyper-cube: • Is surrounded by (8) cubes each one with (6) surfaces. Thus all together, cubes will have (48) surfaces. • Because the cubes wiil slmre surfaces, onlv (24) surfaces will have to be counted effectively. The quaternion-space is spanned by a real unit-vector (e) vertical to a tripod of imaginary unit-vectors {i ^j ^d,}. Among these referencevectors t}re HAMILTONian rules must hold:
References
1. Peitgen, H. O., Jurgens, H., & Saupe, D. (1992). Chaos and Fracal: New Frontiers of Science Springer. New York, p. 9e84.
2. Douady, A., Hubbard, J. H., & Lavaurs, P. (1984). Etude dynamique des polynômes complexes.
3. Mandelbrot, B. B. (1980). Fractal aspects of the iteration of z * Xz(1-z) for complex \ and z. Annals of the New York Academy of Sciences, 357.